Day 2 — Expressions as Algebra: Tokens, Precedence & Postfix (RPN) 🧮

🚀 The Big Idea

Humans read rules with ease. Computers need structure.

When we write something like 👇

score >= 0.85 and (stability > 0.9 or flag == 0)

…it looks natural to us but computers see a tangle of symbols. To evaluate this reliably, we teach machines three steps:

1️⃣ Tokenize – split text into meanings (words, numbers, operators).

2️⃣ Respect precedence – know which operators bind stronger.

3️⃣ Translate to postfix (RPN) – remove parentheses so evaluation is fast and unambiguous.

✨ This gives us rules that are consistent, explainable, and lightning-fast to evaluate.

💡 Where This Appears in Data Science

⚙️ Rule-based labels & weak supervision – define labels from heuristics in a clear, reproducible way.

👥 Cohort & segment definitions – select groups like "(active and high_quality) or (new_user and opted_in)".

🧪 Data-quality & feature checks – guard pipelines with rules like "not null" or value ranges.

📈 Model monitoring & release criteria – e.g. "(precision ≥ X and recall ≥ Y) or (lift ≥ Z)".

🧱 Feature-engineering DSLs – describe derived features safely and consistently.

🧾 Governance & auditability – align rule text with its computation for traceable results.

⚡ Performance & scalability – postfix evaluation runs in O(n) with a tiny stack.

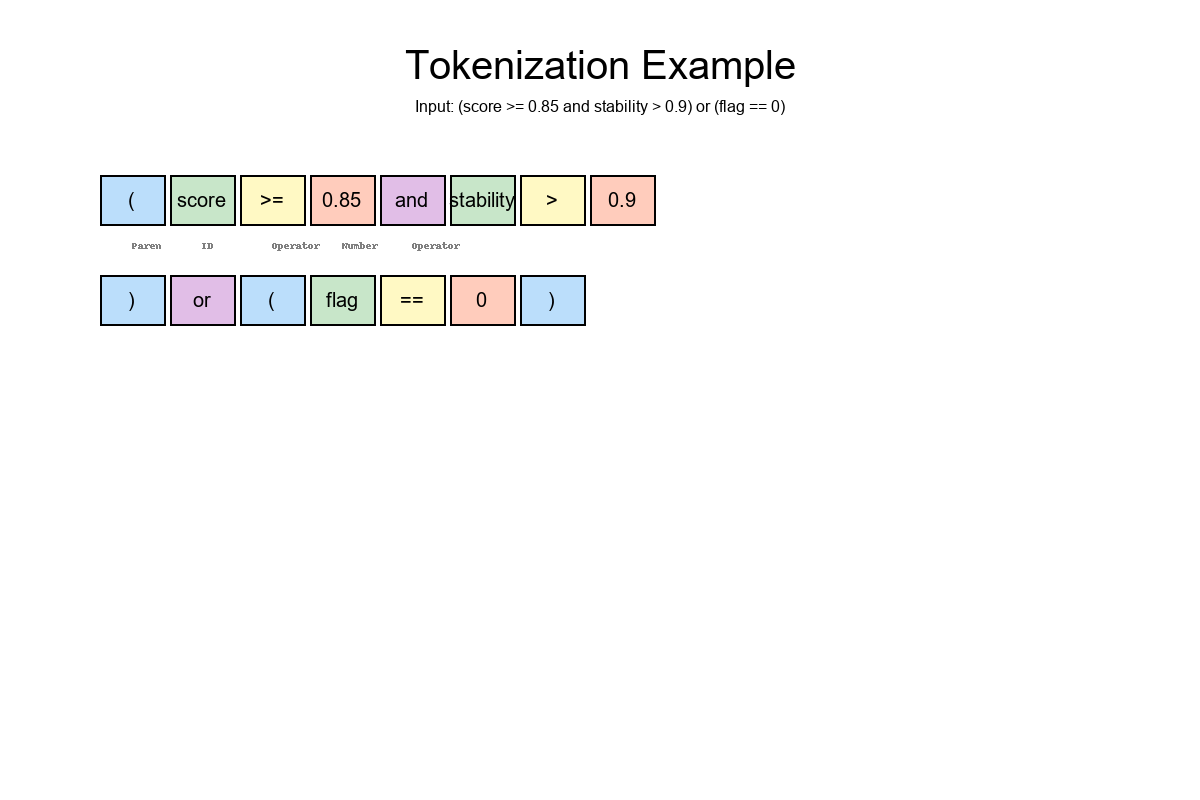
🪄 Step 1 — Tokenize the Rule

Let's start with:

(score >= 0.85 and stability > 0.9) or (flag == 0)

Break it into typed pieces:

🆔 IDs: score, stability, flag

🔢 Numbers: 0.85, 0.9, 0

⚙️ Operators: >=, >, ==, and, or

🧩 Parentheses: (, )

Token stream:

( score >= 0.85 and stability > 0.9 ) or ( flag == 0 )

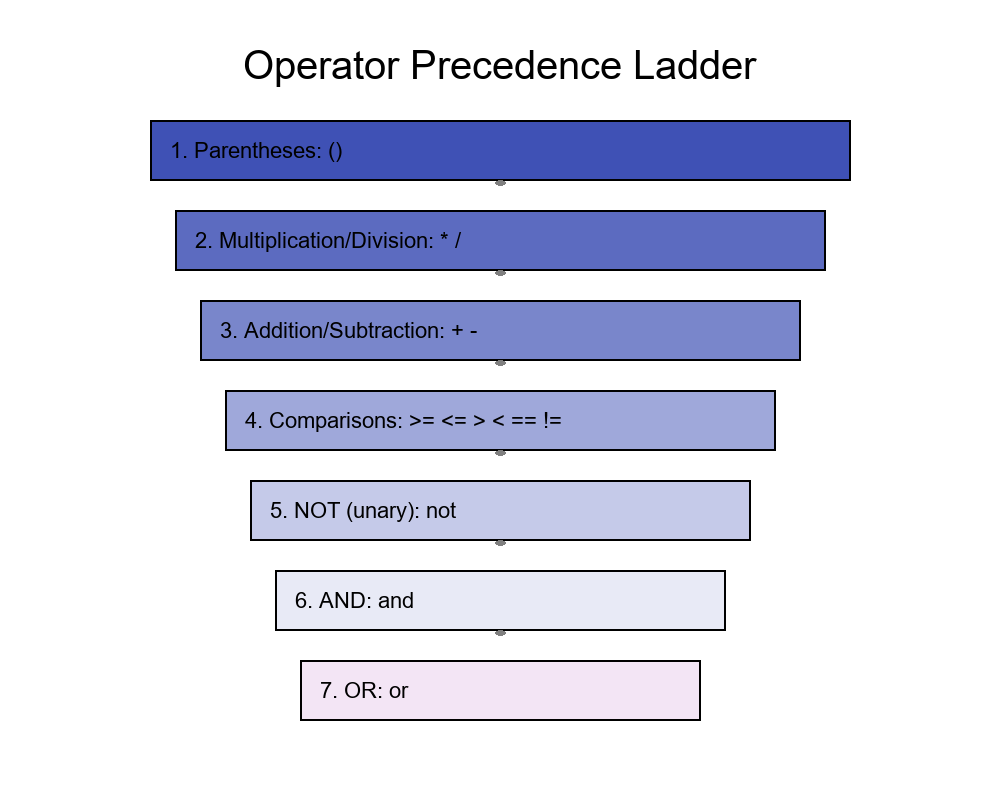
📊 Step 2 — Operator Precedence 🎚️

A consistent order keeps rules predictable (high → low):

1️⃣ * / 2️⃣ + - 3️⃣ Comparisons: >= <= > < == != 4️⃣ not (unary) 5️⃣ and 6️⃣ or

🪶 Parentheses always override everything. Among equals, evaluate left to right.

🔁 Step 3 — Infix → Postfix (RPN) 🚦

Using the shunting-yard algorithm:

• Send values straight to output 🟩
• Push operators on a stack 🗂️
• Pop higher/equal precedence ops before pushing a new one ↕️
• Handle parentheses to group logic () 🎯
• Pop everything left at the end 📤

✅ Our rule becomes:

score 0.85 >= stability 0.9 > and flag 0 == or

Same logic, zero ambiguity. Pure clarity.

🧰 How to Evaluate Postfix

Use a simple stack:

1️⃣ Read left → right. 2️⃣ Push values onto stack. 3️⃣ When you see an operator, pop the needed inputs, apply it, and push the result. 4️⃣ Return the final value (1 for True, 0 for False).

🧮 AND/OR use Boolean logic on those 1s and 0s.

🧩 Worked Example 1 — Full Evaluation

Postfix:

score 0.85 >= stability 0.9 > and flag 0 == or

| Row | score | stability | flag | Result | Explanation | |-----|-------|-----------|------|--------|-------------| | A | 0.86 | 0.91 | 1 | ✅ True | 1 ∧ 1 ∨ 0 = 1 | | B | 0.86 | 0.70 | 0 | ✅ True | 1 ∧ 0 ∨ 1 = 1 | | C | 0.70 | 0.70 | 1 | ❌ False | 0 ∧ 0 ∨ 0 = 0 |

⚖️ Worked Example 2 — Why Precedence Matters

Without parentheses:

score >= 0.85 and stability > 0.9 or flag == 0

Standard ladder → still evaluates as:

(score >= 0.85 and stability > 0.9) or (flag == 0)

💥 Wrong precedence (e.g., "or" before "and") flips results entirely!

🎯 Always follow the ladder —or use explicit brackets.

🧮 Worked Example 3 — With Arithmetic

Infix:

(feature_x / feature_y > 2) and (z_score + bonus >= 3)

Postfix:

feature_x feature_y / 2 > z_score bonus + 3 >= and

| Row | feature_x | feature_y | z_score | bonus | Result | |-----|-----------|-----------|---------|-------|--------| | 1 | 10 | 4 | 2.1 | 1.0 | ✅ True | | 2 | 5 | 4 | 2.5 | 0.2 | ❌ False |

🧯 Tip: guard against division by zero in feature_y.

🚫 Worked Example 4 — Adding Unary not

Infix:

(not drift) and (quality >= 0.95 or coverage >= 0.98)

Postfix:

drift not quality 0.95 >= coverage 0.98 >= or and

| Row | drift | quality | coverage | Result | |-----|-------|---------|----------|--------| | 1 | 1 | 0.97 | 0.90 | ❌ False | | 2 | 0 | 0.93 | 0.99 | ✅ True |

🏁 What You Gain

✅ Consistency – same rule = same result everywhere.

🧠 Simplicity – easy to evaluate and debug.

⚡ Speed – O(n) evaluation with tiny memory footprint.

🔍 Clarity – no hidden precedence surprises.

🧭 Takeaway

Turning rule strings into tokens, honoring a clear precedence order, and evaluating postfix makes your logic solid, predictable, and explainable.

A small engineering habit that scales beautifully from data validation to full-blown rule engines 💪