Day 1 — Boolean Logic to Numbers: AND as min, OR as max 🧮

Binary rules meet graded truth so we can score fuzzy conditions with confidence.

💡 Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.

🎯 Introduction

Business rules rarely stay crisp yes/no. Real pipelines need to score "mostly true" conditions without breaking logical guarantees. Today we upgrade classical Boolean Logic by letting truth values live in the continuous interval [0,1]. To keep intuition, we pick operators that behave just like AND and OR but respect the graded world.

TL;DR:

• Replace AND with the Gödel t-norm min(x,y) and OR with the Gödel t-conorm max(x,y) so logical laws still hold.
• Graded truth lets us evaluate heuristic rules smoothly and conservatively—tightening any condition never increases the score.
• These operators stay interpretable, support complex rule trees, and become the backbone for fuzzy logic and weak-supervision systems.

🚀 About the 30-Day Series

I'm Sughosh P Dixit, Data Scientist at Oracle Finance. This is Day 1 of a 30-day series distilling the math and practical workflows I use every day. Expect:

• Foundational ideas explained with visuals and intuition.
• Real project ties from decision engines to monitoring.
• Hands-on examples and ready-to-use snippets.

Follow along, experiment, and share your takeaways—the goal is to build a robust toolkit together.

🤔 Why go beyond 0 or 1?

Real‑world rules often have shades of satisfaction. For example, two numeric conditions might be "mostly satisfied" rather than strictly true or false. Moving from Boolean 1 to real‑valued [0,1] degrees of truth allows:

• ✅ Graded rule satisfaction ("0.7 satisfied").
• ✅ Smooth aggregation across multiple conditions.
• ✅ Monotone behavior: tightening any input shouldn't increase the rule score.

The central question: how should we generalize AND and OR for values in [0,1]?

T‑norms and T‑conorms at a glance 📐

A t‑norm T generalizes logical AND to [0,1], and a t‑conorm (or s‑norm) S generalizes logical OR. Desiderata for AND‑like T and OR‑like S include:

For a t‑norm T:

• 🔄 Commutativity: T(x,y) = T(y,x)
• 🔗 Associativity: T(x,T(y,z)) = T(T(x,y),z)
• 📈 Monotonicity: if x ≤ x′ and y ≤ y′ then T(x,y) ≤ T(x′,y′)
• 🎯 Neutral element 1: T(x,1) = x

For a t‑conorm S:

• 🔄 Commutativity, associativity, monotonicity
• 🎯 Neutral element 0: S(x,0) = x

Many pairs (T,S) exist. Today's focus is the Gödel pair:

• 🟢 Gödel t‑norm (AND): T(x,y) = min(x,y)
• 🔵 Gödel t‑conorm (OR): S(x,y) = max(x,y)

These are simple, conservative, and highly interpretable.

Gödel AND = min, OR = max ✨

Define, for x,y ∈ [0,1]:

• AND: x ∧ y := min(x,y)
• OR: x ∨ y := max(x,y)

Interpretation: the degree to which both conditions hold is limited by the weaker one; the degree to which at least one holds is governed by the stronger one.

Examples:

• AND: min(0.7, 0.4) = 0.4
• OR: max(0.7, 0.4) = 0.7
• Three inputs: x ∧ y ∧ z = min(x,y,z); x ∨ y ∨ z = max(x,y,z)

Boundary behavior:

• min(x,1) = x; max(x,0) = x
• min(x,0) = 0; max(x,1) = 1

Idempotence:

• min(x,x) = x; max(x,x) = x

Why this is a good generalization of logic 💡

• ✅ If x,y ∈ {0,1}, min/max reduce to classical AND/OR truth tables.
• ✅ Monotonicity: increasing any input cannot decrease OR or increase AND.
• ✅ Conservatism: a weak conjunctive input (near 0) keeps the AND low, as desired.
• ✅ Interpretability: min/max are intuitive aggregators for "all conditions hold" / "at least one holds".

Quick proofs of key properties 📝

Below, write T(x,y) = min(x,y) and S(x,y) = max(x,y). All x,y,z ∈ [0,1].

1️⃣ Commutativity 🔄

min(x,y) = min(y,x)

(symmetric definition), similarly for max. ✓

2️⃣ Associativity 🔗

min(x, min(y,z)) = min(min(x,y), z)

Because min is the least element among {x,y,z}, either side is the minimum of the set. Same for max. ✓

3️⃣ Monotonicity 📈 If x ≤ x′ and y ≤ y′, then min(x,y) ≤ min(x′,y′).

💡 Proof: The minimum cannot increase more than the larger pairwise components; similarly for max.

4️⃣ Neutral elements 🎯

min(x,1) = x

(1 never lowers a minimum)

max(x,0) = x

(0 never lifts a maximum)

5️⃣ Absorption 🔁

min(x, max(x,y)) = x
max(x, min(x,y)) = x

(x always "absorbs" itself.) ✓

6️⃣ Distributivity (over each other) 🎲 On a totally ordered set like the reals in [0,1], min and max distribute over each other:

min(x, max(y,z)) = max(min(x,y), min(x,z))
max(x, min(y,z)) = min(max(x,y), max(x,z))

These are classic lattice identities for totally ordered sets. ✓

Note on "counterexamples": min and max do distribute over each other on a total order. Distributivity fails if you mix different t‑norms/t‑conorms (e.g., product t‑norm with max). See the exercises for a concrete counterexample in that setting.

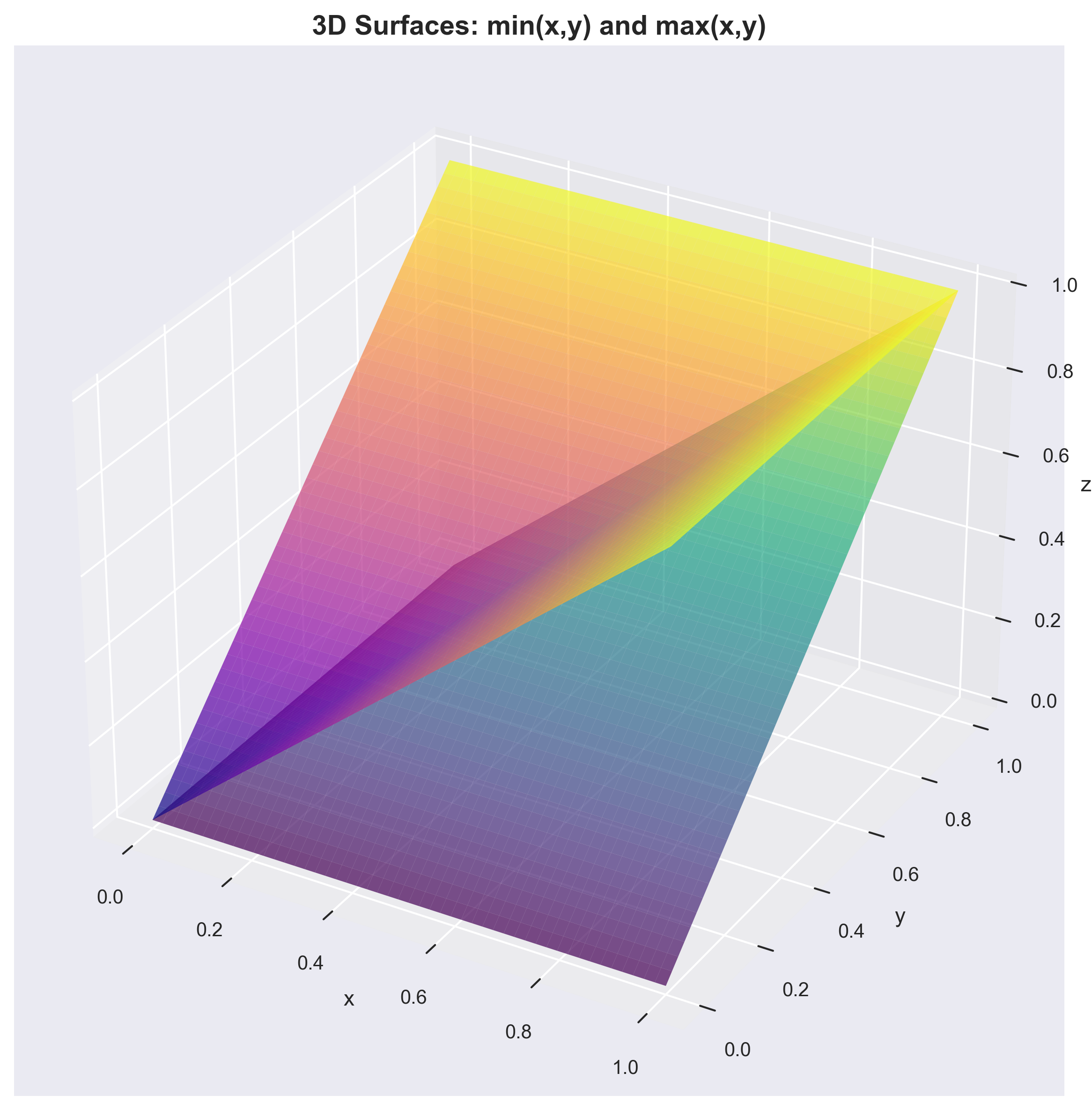
Visual intuition 🎨

• 3D surface of f(x,y)=min(x,y): a saddle‑like surface that follows the lower of the two planes z=x and z=y.
• 3D surface of g(x,y)=max(x,y): the mirror image that follows the higher of z=x and z=y.
• Color maps (x on horizontal, y on vertical): min is dark (low) whenever either axis is low; max is bright (high) whenever either axis is high.

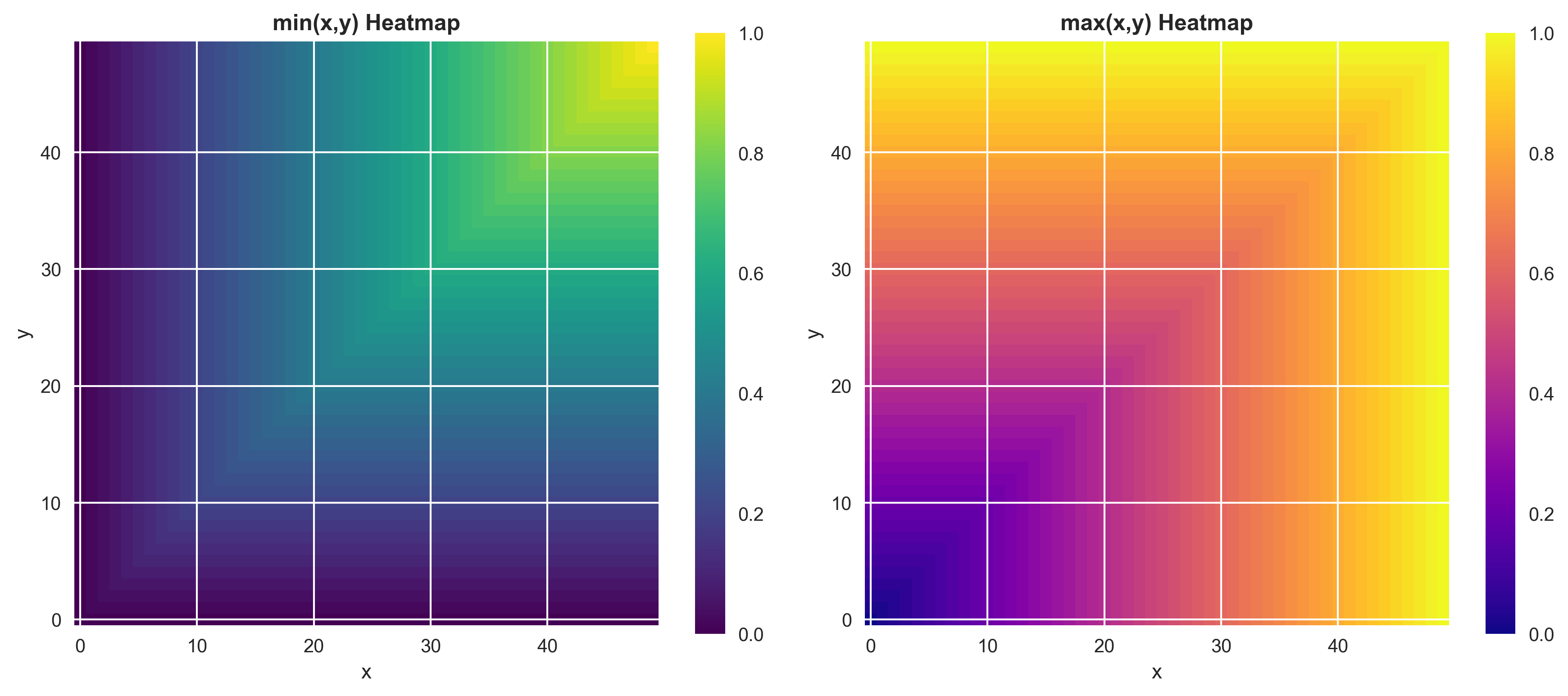
These visuals reinforce how AND is bottlenecked by the weakest input, and OR is lifted by the strongest.

Worked examples 💼

1️⃣ Two‑feature rule: "(A AND B) OR C" 🔀 Using min/max: max(min(A,B), C)

Example 1: If A=0.6, B=0.8, C=0.55

• min(A,B) = 0.6
• OR with C: max(0.6, 0.55) = 0.6 ✓

Example 2: If A=0.6, B=0.2, C=0.55

• min(A,B) = 0.2
• OR with C: max(0.2, 0.55) = 0.55 ✓

2️⃣ Three‑way conjunction: "A AND B AND C" 🔗 Using: min(A,B,C)

• Case 1: (0.7, 0.65, 0.9) → 0.65 ✓
• Case 2: (0.7, 0.65, 0.1) → 0.1 ⚠️ (the weakest link dominates!)

💡 The key insight: AND is bottlenecked by the weakest input; OR is lifted by the strongest input.

How this connects to rule evaluation in practice 🔗

When you write a rule expression (e.g., "feature1 AND (feature2 OR feature3)"), a numeric semantics can evaluate it on scaled numeric inputs. Interpreting AND as min and OR as max makes the rule:

• 📊 Monotone: tightening a threshold for any component cannot falsely inflate the rule score.
• 🎯 Interpretable: the final score is always bounded by the weakest conjunct and supported by the strongest disjunct.
• 🔧 Composable: nested AND/OR become nested min/max, which is associative and easy to compute.

In other words, "logical structure" becomes "min/max algebra," letting you score complex rules consistently on real numbers.

Common alternatives (and why we started with min/max) 🆚

Other popular t‑norms and t‑conorms:

• Product t‑norm: T(x,y)=x·y; Probabilistic sum t‑conorm: S(x,y)=x+y−xy
• Łukasiewicz t‑norm: T(x,y)=max(0, x+y−1); t‑conorm: S(x,y)=min(1, x+y)

These can be smoother or more conservative/aggressive, but min/max are idempotent (T(x,x)=x), preserve ordering cleanly, and exactly recover Boolean logic on 1. They're a standard, robust starting point.

Exercises 📚

1️⃣ Prove the basics ✏️

• Show that min and max satisfy commutativity, associativity, and monotonicity on [0,1].
• Show identity elements: min(x,1)=x and max(x,0)=x.
• Show absorption: min(x, max(x,y)) = x and max(x, min(x,y)) = x.

💡 Hints: Use case splits (x≤y vs y≤x) and the definition of min/max.

2️⃣ Distributivity in a total order 📏

• Prove that for all x,y,z,

  min(x, max(y,z)) = max(min(x,y), min(x,z))
  max(x, min(y,z)) = min(max(x,y), max(x,z))
  

💡 Hint: Reduce to sorted triples or use lattice theory for totally ordered sets.

3️⃣ A counterexample for mixed operators (bonus) 🧩

• Show that product t‑norm does not distribute over max. Find x,y,z ∈ [0,1] such that

  x·max(y,z) ≠ max(x·y, x·z)
  

📝 Example: take x=0.6, y=0.2, z=0.9.

• Left: 0.6·max(0.2,0.9)=0.6·0.9=0.54
• Right: max(0.6·0.2, 0.6·0.9)=max(0.12, 0.54)=0.54 (this one happens to tie; try x=0.3, y=0.9, z=0.4)

💡 Try several triplets until you find strict inequality; in general the equality need not hold.

4️⃣ Interpreting outputs 🔍 Given A=0.7, B=0.3, C=0.6, compute the rule score for "(A AND B) OR C" under:

• 🟢 Gödel (min/max)
• 🟡 Product t‑norm (AND) + probabilistic sum (OR)

💭 Compare and discuss the differences.

🌟 Takeaway

Replacing AND with min and OR with max gives a mathematically principled way to score rule satisfaction on real data. It preserves the essential logic laws, keeps monotonic behavior, and is easy to visualize and explain—an ideal foundation for building more sophisticated, quantitative rule systems over the rest of this series.

📚 References

1. Klement, E. P., Mesiar, R., & Pap, E. (2013). Triangular Norms. Springer Science & Business Media.

2. Hájek, P. (2013). Metamathematics of Fuzzy Logic (Vol. 4). Springer Science & Business Media.

3. Klir, G. J., & Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall.

4. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338-353.

5. Gödel, K. (1932). Zum intuitionistischen Aussagenkalkül. Anzeiger der Akademie der Wissenschaften in Wien, 69, 65-66.

6. Dubois, D., & Prade, H. (1980). Fuzzy Sets and Systems: Theory and Applications. Academic Press.

7. Schweizer, B., & Sklar, A. (1983). Probabilistic Metric Spaces. North-Holland.

8. Fodor, J., & Roubens, M. (1994). Fuzzy Preference Modelling and Multicriteria Decision Support. Springer Science & Business Media.

9. Yager, R. R. (1980). On a general class of fuzzy connectives. Fuzzy Sets and Systems, 4(3), 235-242.

10. Nguyen, H. T., & Walker, E. A. (2006). A First Course in Fuzzy Logic (3rd ed.). Chapman and Hall/CRC.