Day 2 — Expressions as Algebra: Tokens, Precedence & Postfix (RPN)
Teaching computers to understand expressions!
Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.
Introduction
Humans read rules with ease. Computers need structure.
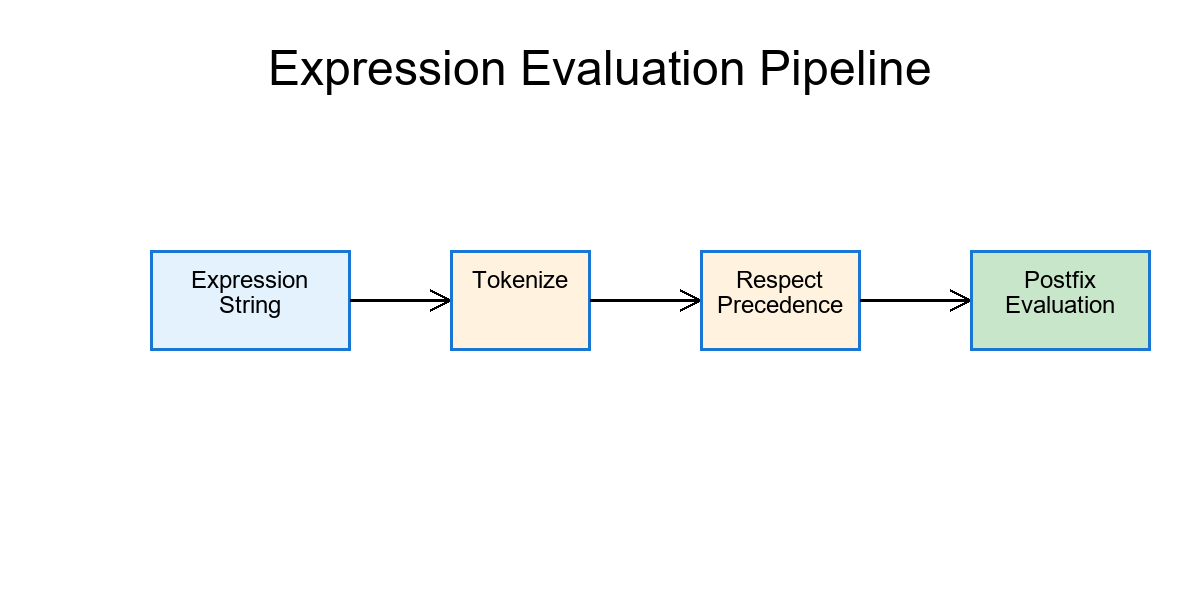
When we write something like score >= 0.85 and (stability > 0.9 or flag == 0), it looks natural to us but computers see a tangle of symbols. To evaluate this reliably, we teach machines three steps: tokenization, operator precedence, and postfix conversion.
TL;DR:
How to teach computers to read and evaluate expressions step by step — by tokenizing text, enforcing operator precedence, and converting rules to postfix (RPN) form for speed, clarity and consistency.
-
Tokenize – split text into meanings (words, numbers, operators).
-
Respect precedence – know which operators bind stronger.
-
Translate to postfix (RPN) – remove parentheses so evaluation is fast and unambiguous.
This gives us rules that are consistent, explainable, and lightning-fast to evaluate.
Where This Appears in Data Science
Rule-based labels & weak supervision – define labels from heuristics in a clear, reproducible way.
Cohort & segment definitions – select groups like "(active and high_quality) or (new_user and opted_in)".
Data-quality & feature checks – guard pipelines with rules like "not null" or value ranges.
Model monitoring & release criteria – e.g. "(precision ≥ X and recall ≥ Y) or (lift ≥ Z)".
Feature-engineering DSLs – describe derived features safely and consistently.
Governance & auditability – align rule text with its computation for traceable results.
Performance & scalability – postfix evaluation runs in O(n) with a tiny stack.
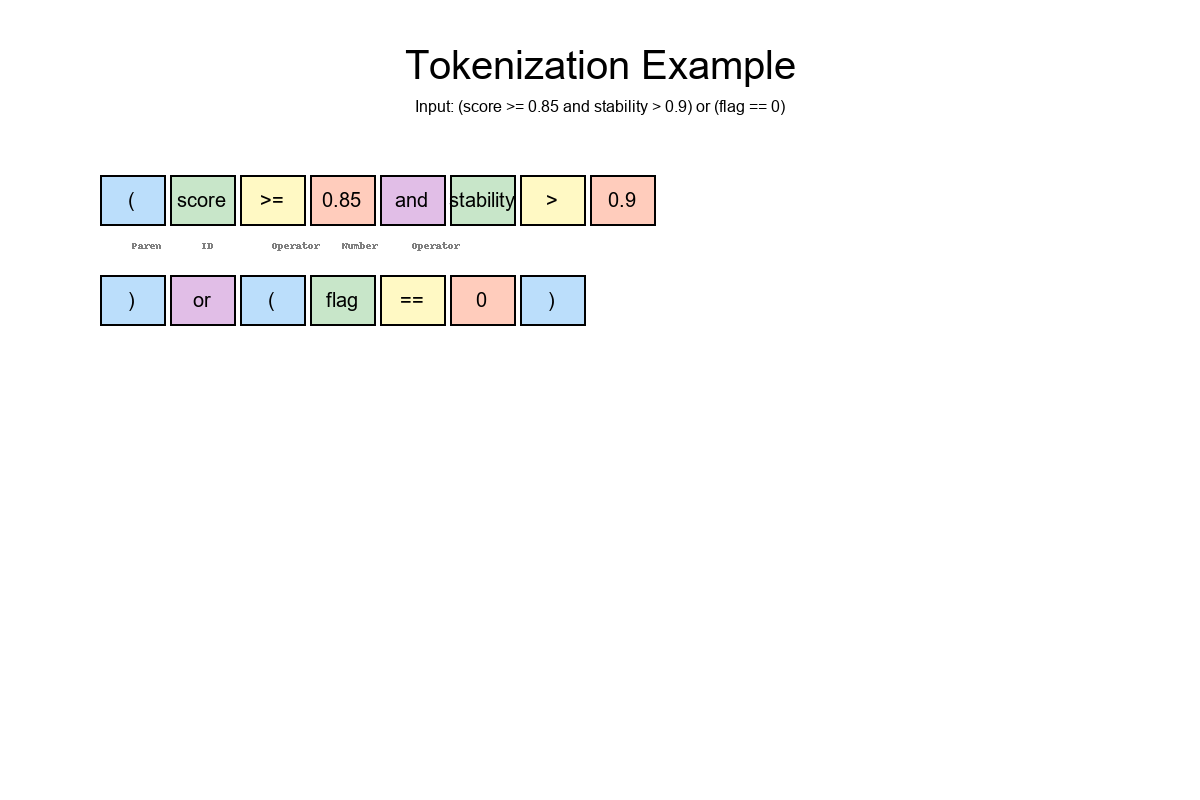
Step 1 — Tokenize the Rule
Let's start with:
(score >= 0.85 and stability > 0.9) or (flag == 0)
Break it into typed pieces:
IDs: score, stability, flag
Numbers: 0.85, 0.9, 0
Operators: >=, >, ==, and, or
Parentheses: (, )
Token stream:
( score >= 0.85 and stability > 0.9 ) or ( flag == 0 )
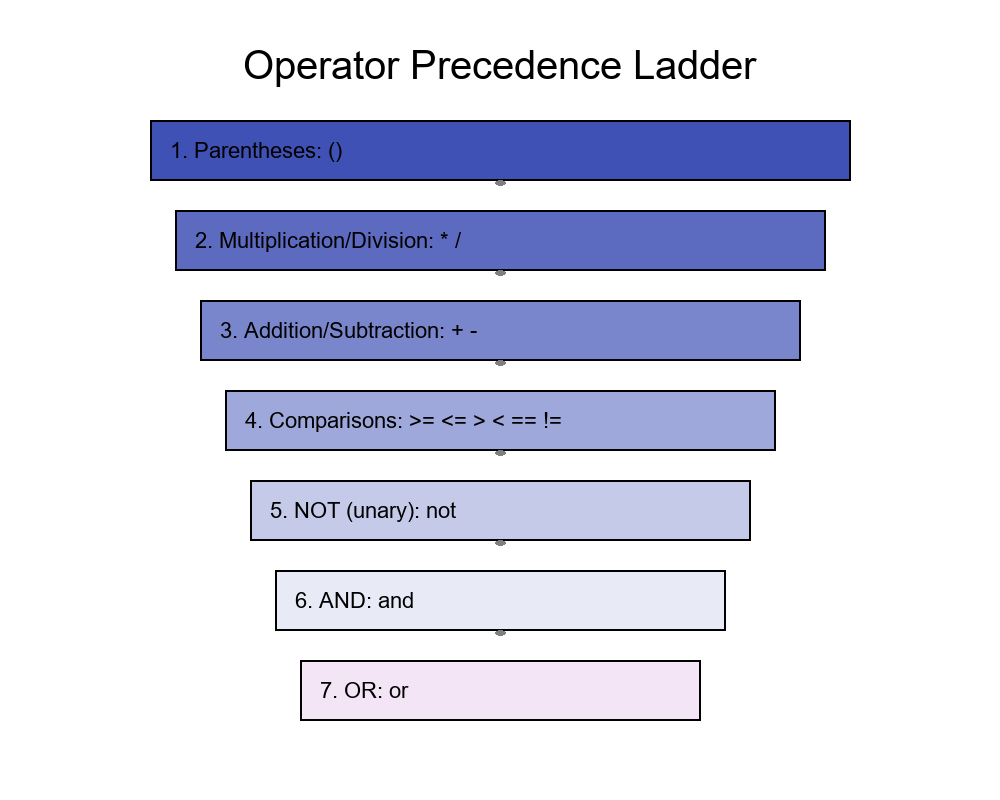
Step 2 — Operator Precedence
A consistent order keeps rules predictable (high → low):
* /+ -- Comparisons:
>= <= > < == != not(unary)andor
Parentheses always override everything. Among equals, evaluate left to right.
Step 3 — Infix → Postfix (RPN)
Using the shunting-yard algorithm:
- Send values straight to output 🟩
- Push operators on a stack
- Pop higher/equal precedence ops before pushing a new one ↕
- Handle parentheses to group logic
() - Pop everything left at the end
Our rule becomes:
score 0.85 >= stability 0.9 > and flag 0 == or
Same logic, zero ambiguity. Pure clarity.

Algorithms make it all work!
How to Evaluate Postfix
Use a simple stack:
- Read left → right.
- Push values onto stack.
- When you see an operator, pop the needed inputs, apply it, and push the result.
- Return the final value (1 for True, 0 for False).
AND/OR use Boolean Logic on those 1s and 0s.
Worked Example 1 — Full Evaluation
Postfix:
score 0.85 >= stability 0.9 > and flag 0 == or
| Row | score | stability | flag | Result | Explanation |
|---|---|---|---|---|---|
| A | 0.86 | 0.91 | 1 | True | 1 ∧ 1 ∨ 0 = 1 |
| B | 0.86 | 0.70 | 0 | True | 1 ∧ 0 ∨ 1 = 1 |
| C | 0.70 | 0.70 | 1 | False | 0 ∧ 0 ∨ 0 = 0 |
Worked Example 2 — Why Precedence Matters
Without parentheses:
score >= 0.85 and stability > 0.9 or flag == 0
Standard ladder → still evaluates as:
(score >= 0.85 and stability > 0.9) or (flag == 0)
Wrong precedence (e.g., "or" before "and") flips results entirely!
Always follow the ladder —or use explicit brackets.
Worked Example 3 — With Arithmetic
Infix:
(feature_x / feature_y > 2) and (z_score + bonus >= 3)
Postfix:
feature_x feature_y / 2 > z_score bonus + 3 >= and
| Row | feature_x | feature_y | z_score | bonus | Result |
|---|---|---|---|---|---|
| 1 | 10 | 4 | 2.1 | 1.0 | True |
| 2 | 5 | 4 | 2.5 | 0.2 | False |
Tip: guard against division by zero in feature_y.
Worked Example 4 — Adding Unary not
Infix:
(not drift) and (quality >= 0.95 or coverage >= 0.98)
Postfix:
drift not quality 0.95 >= coverage 0.98 >= or and
| Row | drift | quality | coverage | Result |
|---|---|---|---|---|
| 1 | 1 | 0.97 | 0.90 | False |
| 2 | 0 | 0.93 | 0.99 | True |
What You Gain
Consistency – same rule = same result everywhere.
Simplicity – easy to evaluate and debug.
Speed – O(n) evaluation with tiny memory footprint.
Clarity – no hidden precedence surprises.
Takeaway
Turning rule strings into tokens, honoring a clear precedence order, and evaluating postfix makes your logic solid, predictable, and explainable.
A small engineering habit that scales beautifully from data validation to full-blown rule engines
References
-
Aho, A. V., Lam, M. S., Sethi, R., & Ullman, J. D. (2006). Compilers: Principles, Techniques, and Tools (2nd ed.). Pearson Education.
-
Knuth, D. E. (1997). The Art of Computer Programming, Volume 1: Fundamental Algorithms (3rd ed.). Addison-Wesley.
-
Dijkstra, E. W. (1961). Algol 60 translation: An algol 60 translator for the x1. In Automatic Programming Information Centre (pp. 1-7).
-
Shunting Yard Algorithm. (n.d.). In Wikipedia. Retrieved from https://en.wikipedia.org/wiki/Shunting_yard_algorithm
-
Pratt, V. R. (1973). Top down operator precedence. In Proceedings of the 1st Annual ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages (pp. 41-51).
-
Aho, A. V., & Ullman, J. D. (1972). The Theory of Parsing, Translation, and Compiling (Vol. 1). Prentice-Hall.
-
Grune, D., & Jacobs, C. J. (2008). Parsing Techniques: A Practical Guide (2nd ed.). Springer.
-
Wirth, N. (1996). Compiler Construction. Addison-Wesley.
-
Louden, K. C. (1997). Compiler Construction: Principles and Practice. PWS Publishing.
-
Sedgewick, R., & Wayne, K. (2011). Algorithms (4th ed.). Addison-Wesley Professional.