Day 26: From Rules to Fuzzy Logic - Why Min-Max Matters
Compare different t-norm operators and understand why min/max provides conservative, idempotent aggregation.
When combining multiple rule conditions, the choice of aggregation operator matters. Different operators have different mathematical properties that affect how rules behave in edge cases.
Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.
The Problem: Combining Rule Conditions
Scenario: You have a fraud rule with multiple conditions:
IF score > 0.7 AND velocity > 5 AND amount > 1000
THEN flag as suspicious
Question: When conditions have partial truth values (fuzzy values between 0 and 1), how do you combine them?
Options:
- Min: Take the minimum value
- Product: Multiply values together
- Łukasiewicz: max(0, x + y - 1)
Each choice has different properties!
T-Norms: The Mathematical Foundation
What is a T-Norm?
A t-norm (triangular norm) is a binary operation T: [0,1] × [0,1] → [0,1] that generalizes logical AND.
Axioms:
- Commutativity: T(x, y) = T(y, x)
- Associativity: T(x, T(y, z)) = T(T(x, y), z)
- Monotonicity: If x ≤ x', then T(x, y) ≤ T(x', y)
- Boundary: T(x, 1) = x (1 is the identity)
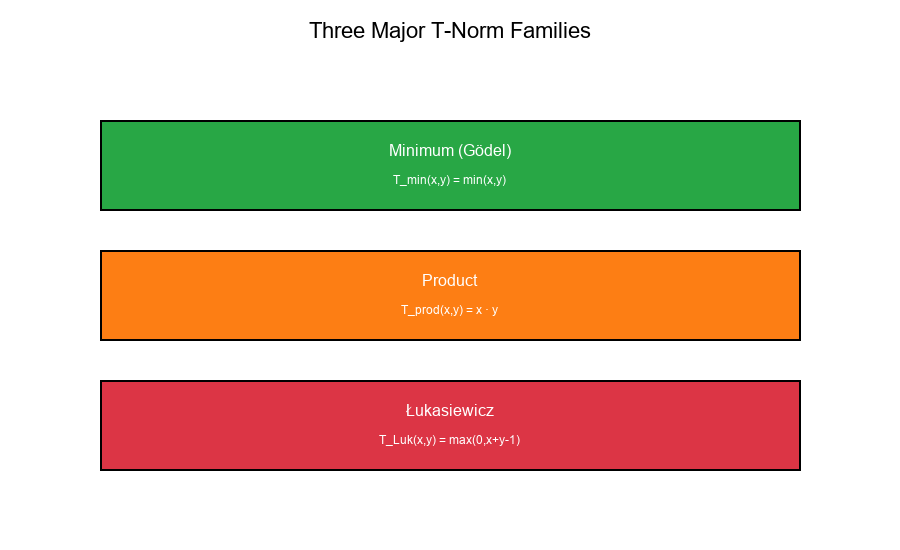
Three Major T-Norm Families
1. Minimum (Gödel):
T_min(x, y) = min(x, y)
2. Product (Probabilistic):
T_prod(x, y) = x · y
3. Łukasiewicz (Bounded):
T_Luk(x, y) = max(0, x + y - 1)
Visual Example:
Comparing T-Norm Behaviors
Numerical Examples
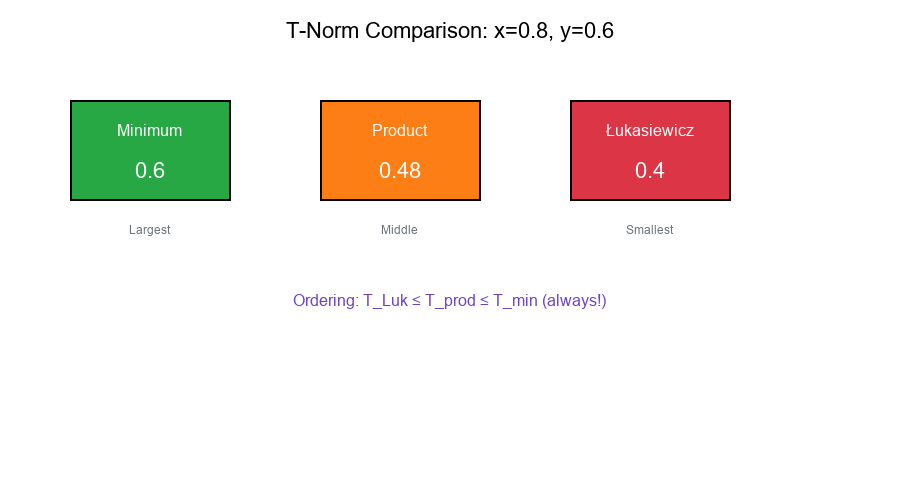
Given: x = 0.8, y = 0.6
| T-Norm | Formula | Result |
|---|---|---|
| Minimum | min(0.8, 0.6) | 0.6 |
| Product | 0.8 × 0.6 | 0.48 |
| Łukasiewicz | max(0, 0.8 + 0.6 - 1) | 0.4 |
Ordering: T_Luk ≤ T_prod ≤ T_min (always!)
Boundary Behaviors
At the extremes:
| Inputs | Min | Product | Łukasiewicz |
|---|---|---|---|
| (1, 1) | 1 | 1 | 1 |
| (1, 0) | 0 | 0 | 0 |
| (0, 0) | 0 | 0 | 0 |
| (0.5, 0.5) | 0.5 | 0.25 | 0 |
Key Observation:
- Min is the most conservative (highest output)
- Łukasiewicz is the most aggressive (lowest output)
- Product is in between
Visual Example:
Surface Comparisons: 3D Visualization
min(x, y) Surface
The minimum function creates a roof-like surface:
- Peak along the diagonal where x = y
- Flat regions where one variable dominates
1
y
0
0 1
x
x · y Surface
The product function creates a curved bowl:
- Smooth hyperbolic shape
- Steeper drop-off than min
max(0, x + y - 1) Surface
The Łukasiewicz function creates a truncated plane:
- Zero below the diagonal x + y = 1
- Linear above the diagonal
Visual Example:

Idempotence: Why Min is Special
What is Idempotence?
An operation T is idempotent if:
T(x, x) = x for all x
Meaning: Combining something with itself doesn't change it.
Testing Idempotence
Minimum:
min(x, x) = x (idempotent!)
Product:
x · x = x² ≠ x (unless x = 0 or x = 1)
Example: 0.5 · 0.5 = 0.25 ≠ 0.5
Łukasiewicz:
max(0, x + x - 1) = max(0, 2x - 1) ≠ x
Example: max(0, 2(0.5) - 1) = 0 ≠ 0.5
Why Idempotence Matters
For rule evaluation:
- Duplicate conditions shouldn't change the result
(A AND A)should equalA- Only min preserves this!
Practical Example:
Show code (9 lines)
# With min (idempotent):
rule_strength = min(0.7, 0.7) # = 0.7
# With product (not idempotent):
rule_strength = 0.7 * 0.7 # = 0.49 (weakened!)
# With Łukasiewicz (not idempotent):
rule_strength = max(0, 0.7 + 0.7 - 1) # = 0.4 (weakened!)
Visual Example:

T-Conorms: The OR Operator
What is a T-Conorm?
A t-conorm (s-norm) generalizes logical OR:
S(x, y) = 1 - T(1-x, 1-y) (De Morgan duality)
Three Major T-Conorms
1. Maximum (dual of min):
S_max(x, y) = max(x, y)
2. Probabilistic Sum (dual of product):
S_prob(x, y) = x + y - x·y
3. Bounded Sum (dual of Łukasiewicz):
S_Luk(x, y) = min(1, x + y)
Comparison
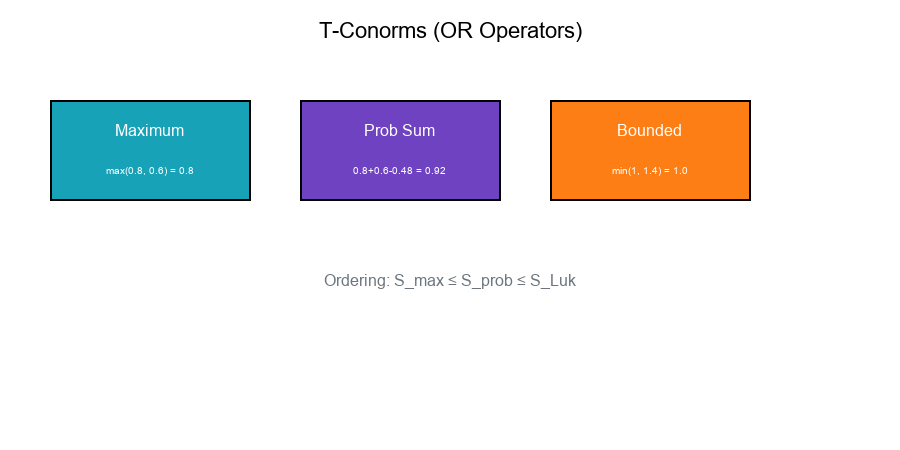
Given: x = 0.8, y = 0.6
| S-Norm | Formula | Result |
|---|---|---|
| Maximum | max(0.8, 0.6) | 0.8 |
| Prob Sum | 0.8 + 0.6 - 0.48 | 0.92 |
| Bounded | min(1, 1.4) | 1.0 |
Ordering: S_max ≤ S_prob ≤ S_Luk
Visual Example:
Application: Rule Strength Aggregation
Using Min/Max for Conservative Aggregation
Why min/max?
- Idempotent: Duplicate conditions don't weaken rules
- Conservative: min gives pessimistic AND, max gives optimistic OR
- Interpretable: Easy to understand and explain
- Stable: Less sensitive to input variations
Example: Fraud Detection Rule
Show code (24 lines)
def evaluate_rule(conditions):
"""
Evaluate rule using min for AND, max for OR.
conditions: List of (value, operator) tuples
"""
and_values = []
or_values = []
for value, op in conditions:
if op == 'AND':
and_values.append(value)
elif op == 'OR':
or_values.append(value)
# Aggregate AND conditions with min
and_result = min(and_values) if and_values else 1.0
# Aggregate OR conditions with max
or_result = max(or_values) if or_values else 0.0
# Combine (depends on rule structure)
return min(and_result, 1 - (1 - or_result))
Practical Example
Show code (14 lines)
# Rule: (high_score AND high_velocity) OR unusual_location
conditions = [
(0.8, 'AND'), # high_score = 0.8
(0.6, 'AND'), # high_velocity = 0.6
(0.9, 'OR'), # unusual_location = 0.9
]
# AND part: min(0.8, 0.6) = 0.6
# OR part: max(0.9) = 0.9
# Combined: max(0.6, 0.9) = 0.9
result = evaluate_rule(conditions) # 0.9
Visual Example:

Exercise: Proving Idempotence Properties
The Problem
Show that:
- Min t-norm is idempotent
- Product t-norm is NOT idempotent (except at boundaries)
Solution
Part 1: Min is Idempotent
Claim: min(x, x) = x for all x ∈ [0, 1]
Proof: By definition of minimum:
min(a, b) = a if a ≤ b
= b if b < a
For a = b = x:
min(x, x) = x (since x ≤ x is always true)
Therefore, min(x, x) = x for all x. ∎
Part 2: Product is NOT Idempotent
Claim: x · x ≠ x for some x ∈ (0, 1)
Proof by counterexample: Let x = 0.5
T_prod(0.5, 0.5) = 0.5 × 0.5 = 0.25 ≠ 0.5
Therefore, product t-norm is not idempotent. ∎
General Case:
x · x = x² = x
x² - x = 0
x(x - 1) = 0
x = 0 or x = 1
Product is idempotent only at the boundary values 0 and 1.
Implications
| Property | Min | Product | Łukasiewicz |
|---|---|---|---|
| Idempotent | Always | Only at 0,1 | Only at 0,1 |
| Conservative | Yes | Reduces | Reduces more |
| Duplicate-safe | Yes | No | No |
Visual Example:

When to Use Each T-Norm
Use Min When:
- Duplicate conditions shouldn't weaken the result
- You want conservative, pessimistic aggregation
- Interpretability is important
- Rule evaluation in fraud detection
Use Product When:
- Conditions are probabilistically independent
- You want to penalize multiple weak conditions
- Bayesian-style reasoning is appropriate
- Classifier combination
Use Łukasiewicz When:
- You want strong conjunction (both must be high)
- Conditions should reinforce each other
- Mathematical properties of bounded logic are needed
- Formal logic applications
Summary Table
| T-Norm | Formula | Idempotent | Behavior |
|---|---|---|---|
| Minimum | min(x, y) | Yes | Conservative, stable |
| Product | x · y | No | Probabilistic, multiplicative |
| Łukasiewicz | max(0, x+y-1) | No | Aggressive, bounded |
Final Thoughts
The choice of aggregation operator has deep mathematical and practical implications. Min/max provides:
- Stability: Idempotence prevents degradation
- Interpretability: Easy to explain to stakeholders
- Conservatism: Safe default for critical applications
Key Takeaways:
T-norms generalize AND for fuzzy values Min is idempotent — duplicates don't weaken Product reduces — x·x = x² < x Łukasiewicz is most aggressive — strongest reduction Min/max for conservative aggregation in rule evaluation Surface visualization reveals operator differences
Choose your operator wisely!
Tomorrow's Preview: Day 27 - Quantile Stability, Ties, and Small Samples