Day 25: Configuration Pairing Logic and Equivalence Classes
Pair semantically complementary sets and ensure consistency across segment configurations.
When working with segmented classification systems, ensuring consistency between paired segments is crucial. Equivalence relations and pairing logic provide the mathematical foundation for this alignment.
Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.
The Problem: Complementary Segments Need Alignment
Scenario: Your classification system has complementary segment pairs:
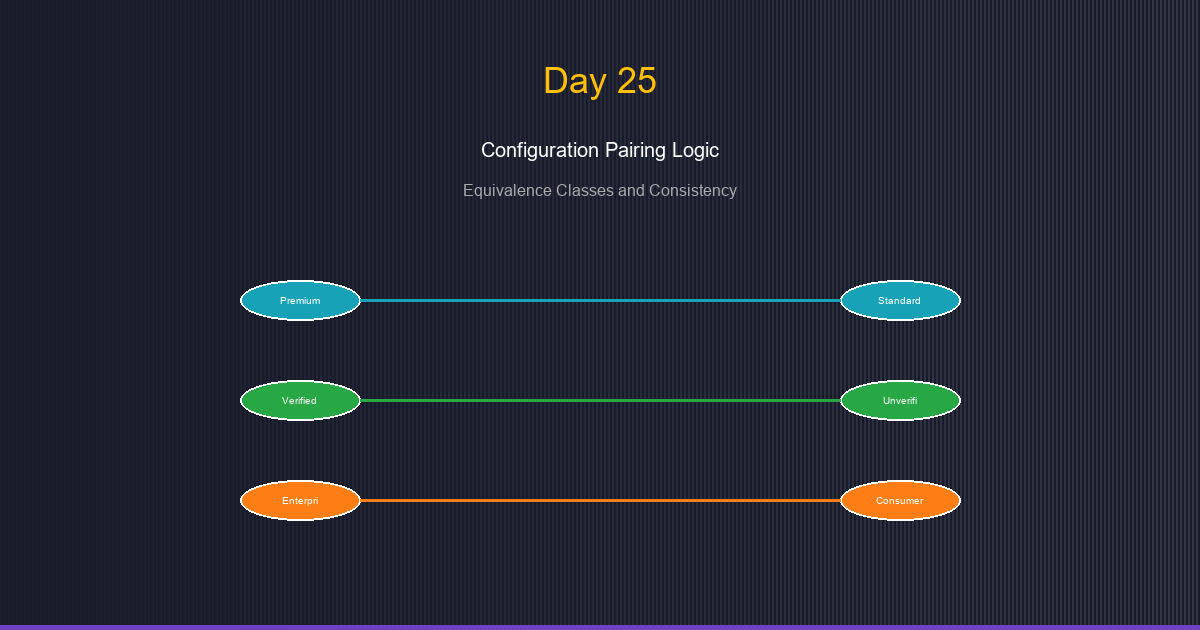
- Premium / Standard (membership tier)
- Verified / Unverified (validation status)
- Enterprise / Consumer (customer type)
Challenge: Each pair must have:
- Consistent structure — Same parameters defined
- Logical completeness — Every entity falls into one category
- Aligned configurations — Compatible handling logic
Question: How do we formally define and validate these pairings?
Equivalence Relations: The Foundation
What is an Equivalence Relation?
An equivalence relation ∼ on a set S satisfies three properties:
- Reflexive: a ∼ a (every element relates to itself)
- Symmetric: If a ∼ b, then b ∼ a
- Transitive: If a ∼ b and b ∼ c, then a ∼ c
Equivalence Classes
An equivalence class [a] contains all elements equivalent to a:
[a] = { x ∈ S : x ∼ a }
Key Property: Equivalence classes partition the set:
- Every element belongs to exactly one class
- Classes are disjoint (no overlap)
- Union of all classes = entire set
Example: Segment Pairing
Set S: All possible segment configurations
Relation ∼: "is a complement of"
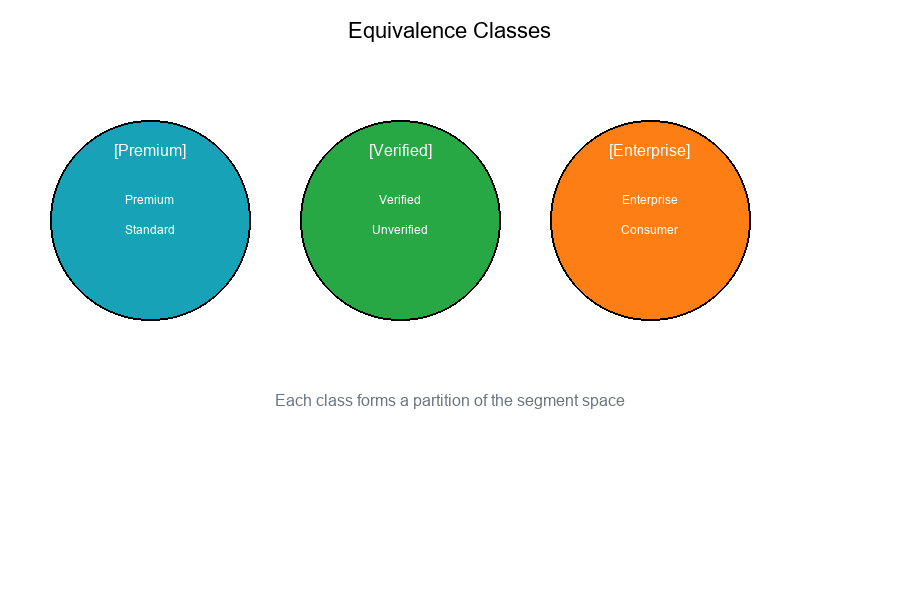
Equivalence Classes:
[Premium] = { Premium, Standard }
[Verified] = { Verified, Unverified }
[Enterprise] = { Enterprise, Consumer }
Visual Example:
Pairing Consistency
What is Pairing Consistency?
Pairing consistency ensures that paired segments have compatible configurations.
Requirements:
- Same parameter set — Both segments define the same parameters
- Complementary coverage — Together they cover all cases
- No contradictions — Rules don't conflict
Formal Definition
Let P = (A, B) be a pair of complementary segments.
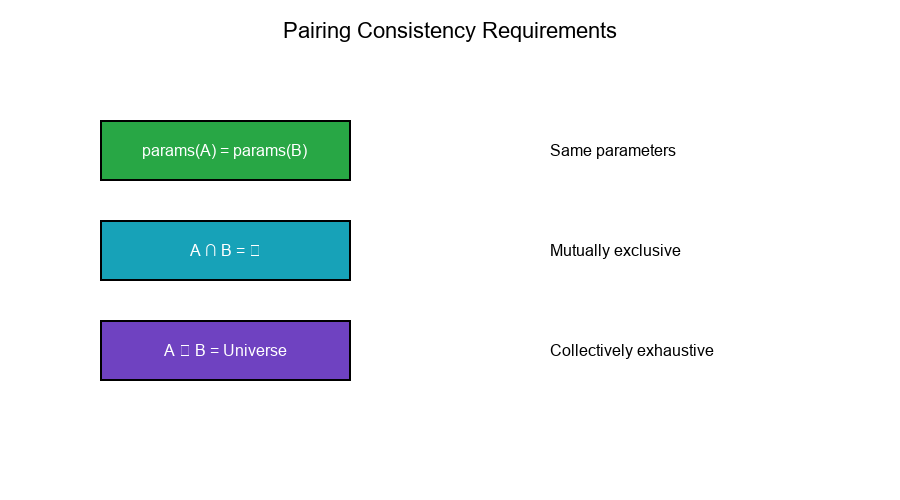
Consistency Conditions:
1. params(A) = params(B) (same parameter names)
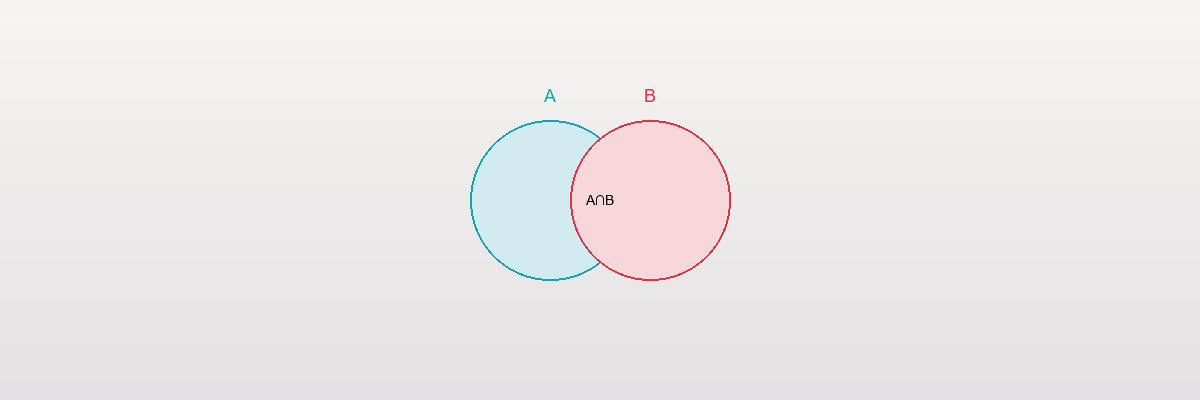
2. A ∩ B = ∅ (mutually exclusive)
3. A ∪ B = Universe (collectively exhaustive)
Example: Premium vs Standard
Premium Configuration:
premium_config = {
'min_membership_days': 180, # days
'score_low': 0.3,
'score_high': 0.7,
'priority_levels': ['Low', 'Medium', 'High']
}
Standard Configuration:
standard_config = {
'min_membership_days': 0, # days (different value, same param)
'score_low': 0.2, # lower score (more conservative)
'score_high': 0.6,
'priority_levels': ['Low', 'Medium', 'High'] # same levels
}
Consistency Check:
- Same parameters defined
- Mutually exclusive (days < 180 vs days ≥ 180)
- Covers all members
Visual Example:
Mapping Functions: Aligning Parameters
The Role of Mapping Functions
Mapping functions translate parameters between paired segments to ensure alignment.
Purpose:
- Handle naming differences
- Apply transformations
- Fill in missing values
translate_bindings Function
Show code (25 lines)
def translate_bindings(source_config, target_segment, mapping_rules):
"""
Translate configuration from source to target segment.
Parameters:
- source_config: Configuration dictionary
- target_segment: Target segment name
- mapping_rules: Dictionary of parameter mappings
Returns:
- Translated configuration for target segment
"""
translated = {}
for param, value in source_config.items():
if param in mapping_rules:
rule = mapping_rules[param]
new_param = rule.get('rename', param)
transform = rule.get('transform', lambda x: x)
translated[new_param] = transform(value)
else:
translated[param] = value
return translated
Example: Parameter Mapping
Mapping Rules:
Show code (11 lines)
mapping_rules = {
'score_low': {
'rename': 'score_low',
'transform': lambda x: x * 0.8 # Standard gets 80% of score
},
'score_high': {
'rename': 'score_high',
'transform': lambda x: x * 0.9 # Standard gets 90% of score
}
}
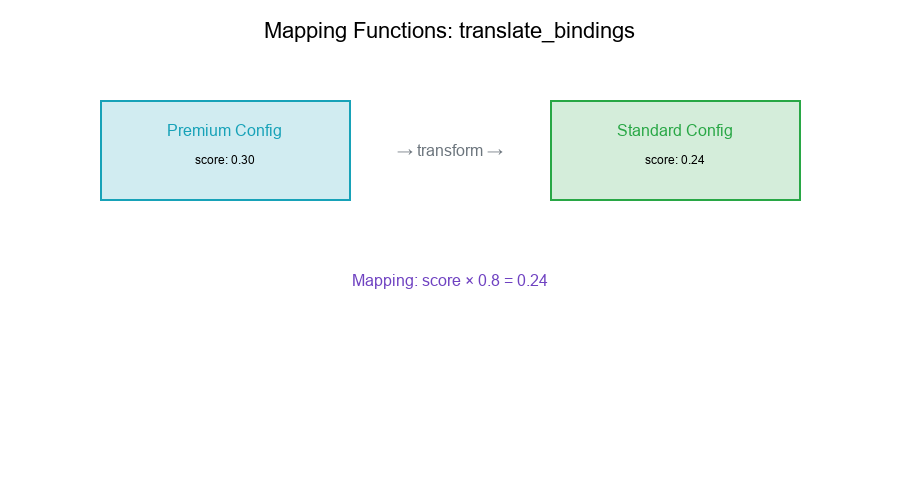
Application:
premium = {'score_low': 0.30, 'score_high': 0.70}
standard = translate_bindings(premium, 'Standard', mapping_rules)
# Result: {'score_low': 0.24, 'score_high': 0.63}
Visual Example:
Bipartite Graph Matching
Visualizing Pairings as Graphs
Bipartite graph: A graph where vertices can be divided into two disjoint sets, with edges only between sets.
For segment pairing:
- Set A: Primary segments (Premium, Verified, Enterprise)
- Set B: Complement segments (Standard, Unverified, Consumer)
- Edges: Pairing relationships
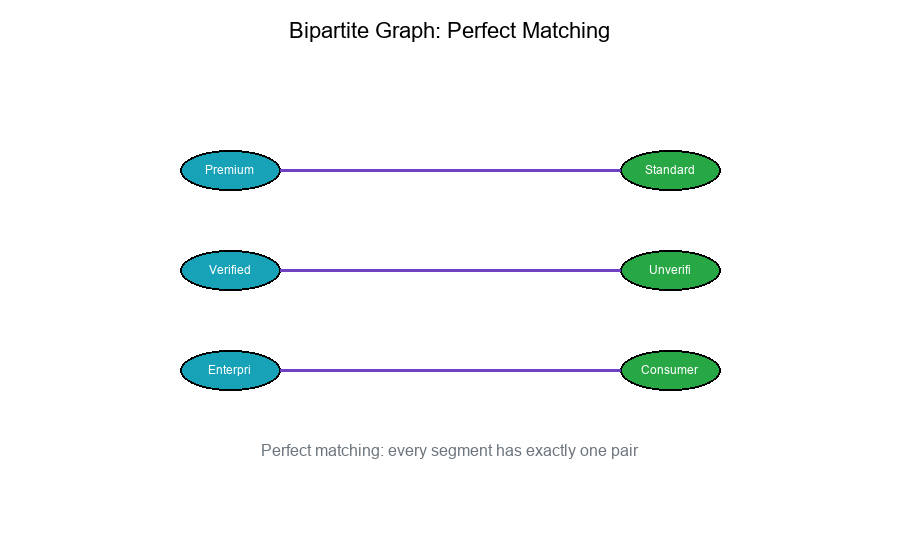
Perfect Matching
A perfect matching in a bipartite graph:
- Every vertex in A is matched to exactly one vertex in B
- Every vertex in B is matched to exactly one vertex in A
- No unmatched vertices
For segment pairing: A perfect matching ensures every segment has exactly one complement.
Example: Segment Matching
Primary Segments Complement Segments
Premium ←→ Standard
Verified ←→ Unverified
Enterprise ←→ Consumer
Visual Example:
validate_and_pair_segments Function
Purpose
The validate_and_pair_segments function:
- Validates that all required pairs exist
- Checks consistency between paired segments
- Identifies missing or orphan segments
- Returns validated pairings
Implementation Concept
Show code (41 lines)
def validate_and_pair_segments(segment_configs, pairing_rules):
"""
Validate and pair segment configurations.
Parameters:
- segment_configs: Dict of segment -> config
- pairing_rules: List of (primary, complement) tuples
Returns:
- validated_pairs: List of validated (primary, complement) pairs
- errors: List of validation errors
"""
validated_pairs = []
errors = []
for primary, complement in pairing_rules:
# Check both segments exist
if primary not in segment_configs:
errors.append(f"Missing primary segment: {primary}")
continue
if complement not in segment_configs:
errors.append(f"Missing complement segment: {complement}")
continue
# Check parameter consistency
primary_params = set(segment_configs[primary].keys())
complement_params = set(segment_configs[complement].keys())
if primary_params != complement_params:
missing = primary_params - complement_params
extra = complement_params - primary_params
errors.append(f"Parameter mismatch: {primary}/{complement}")
errors.append(f" Missing in complement: {missing}")
errors.append(f" Extra in complement: {extra}")
continue
# All checks passed
validated_pairs.append((primary, complement))
return validated_pairs, errors
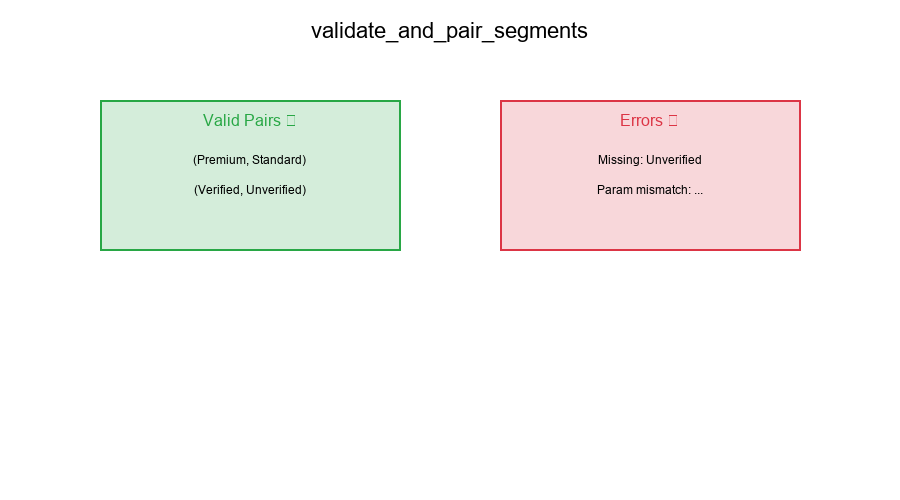
Example Usage
Show code (13 lines)
configs = {
'Premium': {'score': 0.5, 'levels': ['L', 'M', 'H']},
'Standard': {'score': 0.4, 'levels': ['L', 'M', 'H']},
'Verified': {'score': 0.6, 'levels': ['L', 'M', 'H']},
# Missing 'Unverified'!
}
rules = [('Premium', 'Standard'), ('Verified', 'Unverified')]
pairs, errors = validate_and_pair_segments(configs, rules)
# pairs: [('Premium', 'Standard')]
# errors: ['Missing complement segment: Unverified']
Visual Example:
Exercise: Floor Fill-In for Missing Priority Levels
The Problem
Theorem: Consistent pairing implies well-defined floor fill-in for missing priority levels.
Claim: If segments A and B are consistently paired, and A defines parameters for priority levels {L, M, H}, then missing parameters in B can be filled using A's values as a floor.
Prove this property.
Solution
Step 1: Define Consistent Pairing
Segments A and B are consistently paired if:
- params(A) = params(B) (same parameter names)
- levels(A) = levels(B) (same priority categories)
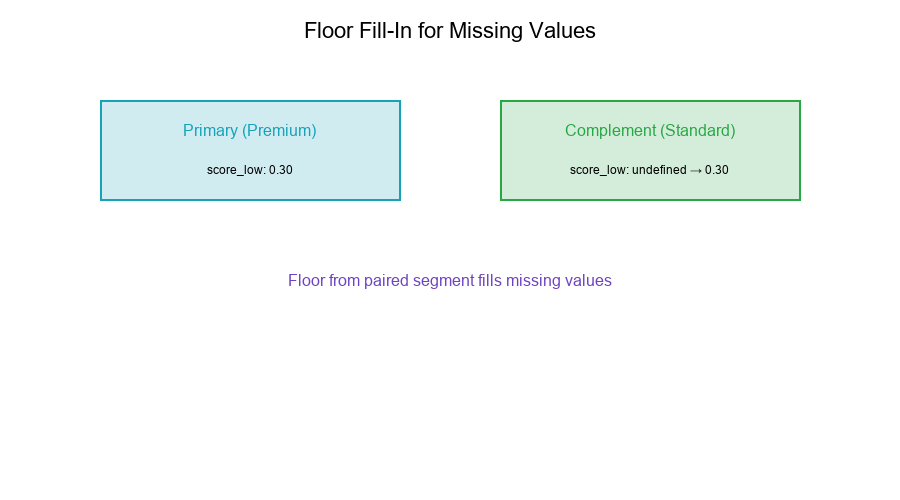
Step 2: Define Floor Fill-In
For any parameter p and priority level r:
B[p, r] = B[p, r] if defined
= A[p, r] if B[p, r] undefined (floor from A)
Step 3: Prove Well-Definedness
Assume consistent pairing. For any (p, r):
Case 1: B[p, r] is defined
- Use B[p, r] directly
Case 2: B[p, r] is undefined
- By consistent pairing, A defines the same parameters
- Therefore A[p, r] is defined
- Use A[p, r] as floor
Step 4: Uniqueness
The fill-in is unique because:
- If B[p, r] defined → use it (no choice)
- If B[p, r] undefined → use A[p, r] (no ambiguity)
Step 5: Conclusion
Consistent pairing guarantees:
- Every parameter in B has a well-defined value
- The floor comes from the paired segment A
- No ambiguity or undefined cases
∴ Floor fill-in is well-defined under consistent pairing. ∎
Practical Implication
Show code (12 lines)
def fill_missing_params(primary_config, complement_config):
"""
Fill missing parameters in complement using primary as floor.
"""
filled = complement_config.copy()
for param, value in primary_config.items():
if param not in filled or filled[param] is None:
filled[param] = value # Floor fill-in
return filled
Visual Example:
Best Practices for Segment Pairing
1. Define Explicit Pairing Rules
Document which segments are paired:
PAIRING_RULES = [
('Premium', 'Standard'),
('Verified', 'Unverified'),
('Enterprise', 'Consumer'),
]
2. Validate Early and Often
Run validation on every configuration change:
pairs, errors = validate_and_pair_segments(configs, PAIRING_RULES)
if errors:
raise ConfigurationError(errors)
3. Use Mapping Functions for Transformations
Don't manually duplicate with modifications:
# Good: Use mapping
standard = translate_bindings(premium, 'Standard', rules)
# Bad: Manual duplication
standard = {'score': premium['score'] * 0.8, ...}
4. Document Fill-In Logic
Make floor fill-in explicit:
# Floor from Premium if Standard is missing
FLOOR_HIERARCHY = {
'Standard': 'Premium',
'Unverified': 'Verified',
}
5. Test Edge Cases
- Missing segments
- Extra (orphan) segments
- Parameter mismatches
- Null/undefined values
6. Version Control Pairings
Track changes to pairing rules alongside configuration changes.
Summary Table
| Concept | Definition | Use Case |
|---|---|---|
| Equivalence Relation | Reflexive, symmetric, transitive relation | Grouping complementary segments |
| Equivalence Class | All elements equivalent to each other | Segment pairs form classes |
| Pairing Consistency | Same params, mutually exclusive, exhaustive | Validating segment configurations |
| Mapping Function | Translates params between segments | Aligning paired configurations |
| Bipartite Matching | Perfect pairing between two sets | Ensuring every segment has a pair |
| Floor Fill-In | Use paired segment for missing values | Handling incomplete configs |
Final Thoughts
Segment pairing logic ensures that complementary categories work together consistently. By applying equivalence relations and mapping functions, we create a robust system where:
- Every segment has a well-defined complement
- Parameters align across pairs
- Missing values have principled fill-in
Key Takeaways:
Equivalence relations group complementary segments into classes Pairing consistency ensures compatible configurations Mapping functions translate parameters systematically Bipartite matching visualizes and validates pairings validate_and_pair_segments operationalizes validation Floor fill-in handles missing values from paired segments
Pair your segments, align your configurations!
Tomorrow's Preview: Day 26 - From Rules to Fuzzy Logic: Why Min/Max Matters