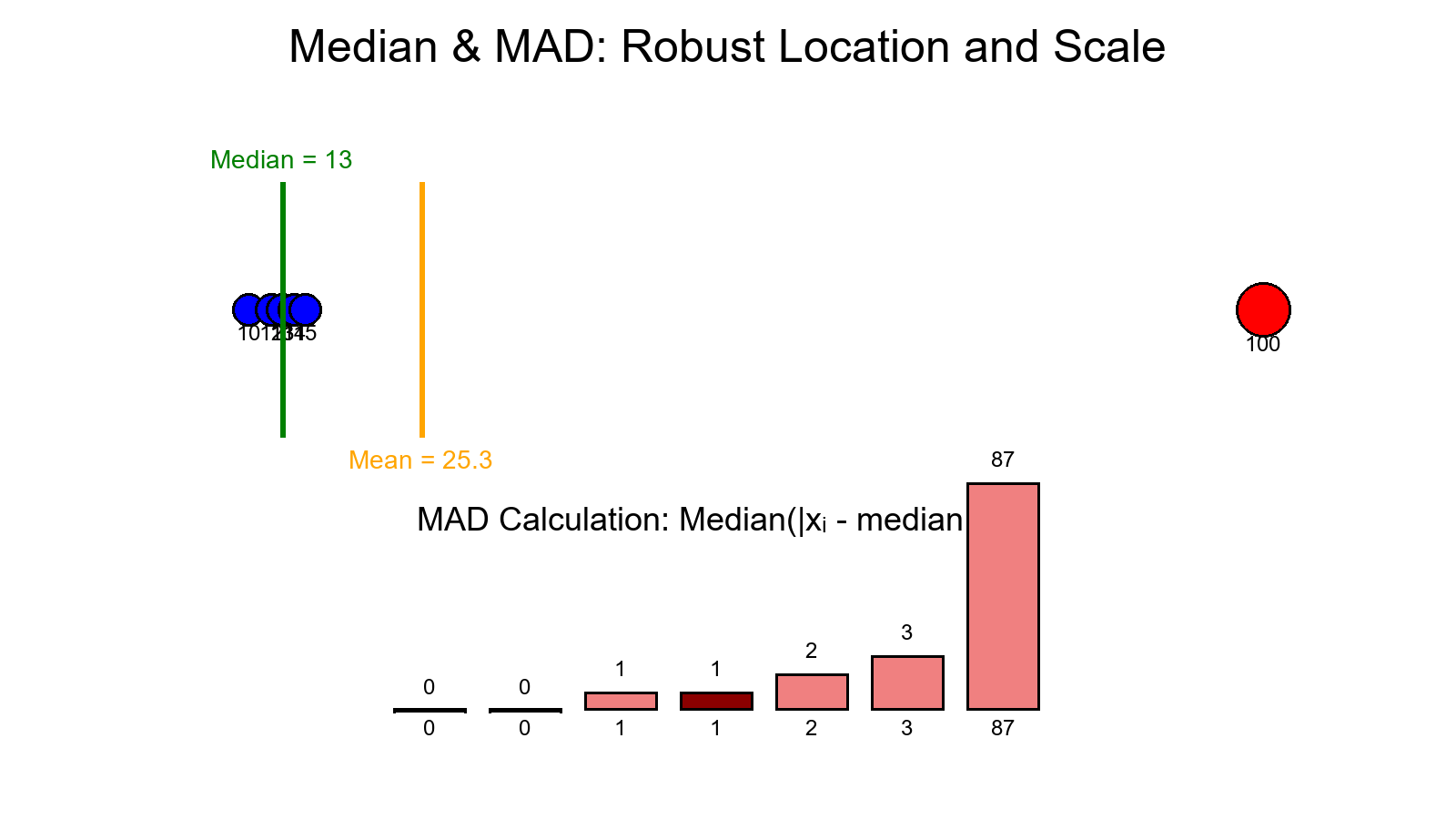
Day 10 — Isolation Forest: Finding Outliers by Getting Lost in the Woods 🌲🔍

Outliers get discovered when they are easy to isolate; normals stay hidden in the crowd.

Isolation Forest hunts anomalies by slicing the feature space into random partitions.

💡 Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.

🎯 Introduction

Isolation Forest flips the usual anomaly detection script: instead of measuring distance or density, it asks how many random splits it takes to isolate each point. Outliers pop out in just a few cuts, while normal observations require long paths.

TL;DR:

• Random, axis-aligned splits form "isolation" trees; the average path length tells us how typical a point is.
• Short paths (few splits) imply highly isolated points → likely anomalies.
• Long paths behave like the expected depth of a random binary search tree → normal behaviour.
• The anomaly score s(x, n) = 2^{-(E[h(x)] / c(n))} normalises path length across dataset sizes.
• Tune the contamination rate, subsample size, and number of trees to balance recall vs. false alarms.

🗺️ The "Lost Tourist" Intuition

Imagine playing hide-and-seek in a forest:

• Normal Nancy 🙋‍♀️ hides in a picnic area with 100 other people.
• Outlier Oliver 🕴️ stands alone on a remote ridge.

Randomly partition the forest ("north vs south", "east vs west"). Oliver becomes isolated after two or three cuts, while Nancy remains grouped through many partitions. That isolation speed is the entire idea behind Isolation Forest.

Normal zone:  ██████████████  (dozens of points)
Outlier zone:      ●          (one lonely point)

Random splits isolate sparse regions quickly; dense regions take far more steps.

🌳 Isolation Trees vs. Classification Trees

Classical decision trees predict labels; every split is chosen to maximise purity. Isolation trees do the opposite: they pick a random feature and a random split value purely to fragment the data. Isolation depth (the number of splits required before a point is alone) becomes the signal.

Key contrasts:

• No optimisation of Gini/entropy — randomness drives diversity.
• Trees stop when a point is isolated or the height limit ⌈log₂ ψ⌉ is reached.
• We average across many shallow trees (typically 100) to get a stable expectation.

🔁 Algorithm in Plain English

1. Sample ψ points (default 256) without replacement.
2. Pick a random feature.
3. Draw a split uniformly between that feature's min and max within the sample.
4. Partition the sample and recurse on each side.
5. Stop when a leaf contains one point or the recursion depth hits ⌈log₂ ψ⌉.

Outliers that live alone in feature space travel short paths; normals buried in dense regions take ~log(ψ) splits.

📊 A Tiny 2D Example

Consider a toy dataset with one obvious outlier:

         Feature 2 (Y)
              ↑
          10  |     •  (outlier)
              |
           8  |
              |
           6  |   •  •  •
              |   • •• ••
           4  |   •• • •
              |   •••••
           2  |   •• ••
              |
           0  └────────────→ Feature 1 (X)
                 0  2  4  6  8

• Split 1: choose Y = 9. The lone point is already isolated → path length 1.
• Normal point: it takes many more splits (random X, random Y) to single out a dense point.

Isolation Forest records these path lengths across many trees and averages them into E[h(x)].

🧮 Why Short Paths Flag Anomalies

Let h(x) be the length of the path taken by point x in one isolation tree. The expected path length over many random trees resembles the average depth of a node in a random binary search tree.

For a sample size n the expected path length for a normal observation is:

c(n) = 2 H(n-1) - 2 (n-1)/n

where H(k) is the harmonic number 1 + 1/2 + … + 1/k.

• Harmonic numbers grow like log(k) + γ (γ is the Euler–Mascheroni constant).
• Thus c(n) ≈ 2 log(n), matching the depth of random binary trees and quicksort comparisons.
• If h(x) is much smaller than c(n), the point behaves like an outlier.

Example (n = 100):

H(99) ≈ 5.177
c(100) = 2 × 5.177 − 2(99)/100 ≈ 8.37

A point isolated in 2–3 splits is far below 8.37 — suspicious!

🎯 The Anomaly Score

Isolation Forest converts path lengths into a unitless score:

s(x, n) = 2^{-(E[h(x)] / c(n))}

• E[h(x)] — average path length for point x across all trees.
• c(n) — expected path length for normal data of size n.
• The base 2 exponent mirrors the probability of surviving independent random splits.

Interpretation:

• s(x) ≈ 1 → extremely short path → strong anomaly.
• s(x) ≈ 0.5 → average path → nominal.
• s(x) < 0.5 → longer-than-expected path → deeply embedded in the population.

🏗️ Training & Scoring Pipeline

Training

• Subsample size ψ (often 256) keeps trees shallow and fast.
• Build t isolation trees (100–200 is common).
• Stop recursion early when a node contains one point or depth exceeds ⌈log₂ ψ⌉.

Scoring

• Drop each candidate point through every tree and measure hᵢ(x).
• Average path lengths → E[h(x)].
• Compute anomaly score s(x, n) using the formula above.
• Threshold scores based on the expected contamination rate.

🎮 Hand-Isolating an Extreme Point

Dataset:

Points = [(2,3), (3,3), (2,4), (3,4), (2,5), (3,5), (15,15)]

Step 1 — Isolate the obvious outlier (15,15)

• Split on X = 8 → right branch contains only (15,15).
• Path length = 1 (outlier detected).

Step 2 — Isolate a normal point (2,3)

• Split on X = 2.5 → left branch has three points.
• Split on Y = 3.5 → (2,3) is finally alone.
• Path length = 2 (still short, but longer than the true outlier).

Increasing the population to hundreds of normal points would push the expected path length toward 2 log(n), while the outlier remains almost unchanged.

🐍 Python Implementation

from sklearn.ensemble import IsolationForest

def isolation_forest_outliers(data, contamination=0.1, random_state=42):
    """Return suspected outliers and anomaly scores using Isolation Forest."""
    iso_forest = IsolationForest(
        n_estimators=100,
        max_samples=256,
        contamination=contamination,
        random_state=random_state
    )

    predictions = iso_forest.fit_predict(data)  # -1 = outlier, 1 = normal
    scores = iso_forest.score_samples(data)     # More negative = more anomalous

    outliers = data[predictions == -1]
    return outliers, scores

• contamination sets the expected proportion of anomalies and controls the score threshold.
• Inspect both predictions and scores; scores allow custom thresholds or ranking.

🎚️ Tuning the Contamination Rate

• Start with 0.1 if you have no prior — it flags the top 10 % highest scores.
• Lower to 0.01 for fraud/rare-event detection; raise to 0.2 for exploratory triage.
• Always validate against domain knowledge: review a few flagged examples and iterate.

🌲 Short vs. Long Paths at a Glance

• Outliers separate in a handful of cuts.
• Normals stay within dense groups and accumulate depth quickly.

⭐ Strengths

• Distribution free: no Gaussian assumptions required.
• Scales to high dimensions: random feature selection tempers the curse of dimensionality.
• Fast: O(t × ψ × log ψ) training; linear in number of trees.
• Works with numeric + ordinal features without heavy preprocessing.
• Easy to explain: "it took 2 cuts to isolate this point, normals take ~8".

⚠️ Limitations & Gotchas

• Requires a good guess of the expected outlier rate (contamination).
• Random splits can behave poorly on strongly clustered, imbalanced data.
• Provides a binary outlier flag, not feature-level explanations.
• Sensitive to duplicate points — heavy duplicates can shorten paths artificially.
• Not ideal for very small samples (n < 100); use robust statistics instead.

📊 Method Comparison Snapshot

| Method | Speed | Works in High-d | Finds Local Outliers | Explainability | |--------|-------|-----------------|----------------------|----------------| | Z-score | ⚡⚡⚡ | ❌ | Global only | ⭐⭐⭐ | | IQR / Tukey fences | ⚡⚡⚡ | ❌ | Global only | ⭐⭐⭐ | | Isolation Forest | ⚡⚡ | ✅ | Global | ⭐⭐ | | LOF (Day 11) | ⚡ | ❌ | Local | ⭐ | | DBSCAN | ⚡⚡ | ❌ | Local clusters | ⭐⭐ |

🎯 When to Reach for Isolation Forest

Use it when:

• You have thousands of observations and many features.
• You expect global anomalies that sit far from all clusters.
• You need a quick, tunable outlier score for triage pipelines.
• You want to augment fraud, intrusion, or sensor monitoring systems.

Look elsewhere when:

• You have very few observations — prefer robust z-scores or Tukey fences.
• Anomalies are local (weird only within a neighbourhood) — try LOF or DBSCAN.
• You need feature-level reasons — combine with SHAP, anchors, or rule-based checks.

💡 Pro Tips

1. Use at least 100 trees; 200+ stabilises results on noisy data.
2. Keep max_samples at 256 unless you have massive data — it preserves randomness.
3. Compare score quantiles against expectations; adjust contamination iteratively.
4. Combine with domain filters (e.g., known bad ranges) for higher precision.
5. Log both scores and feature values for diagnostics; short paths without context can be misleading.
6. Validate on historical incidents; measure precision/recall before deployment.

🌟 Takeaway

Isolation Forest detects anomalies by counting how often points get "lost in the woods." If it takes far fewer splits than the population average, the point is almost certainly unusual. With the right contamination setting and a healthy number of trees, it delivers fast, distribution-free anomaly detection for modern pipelines.

📚 References

1. Liu, F. T., Ting, K. M., & Zhou, Z.-H. (2008). Isolation Forest. 2008 Eighth IEEE International Conference on Data Mining, 413–422.
2. Liu, F. T., Ting, K. M., & Zhou, Z.-H. (2012). Isolation-based anomaly detection. ACM Transactions on Knowledge Discovery from Data, 6(1), 3.
3. Zhou, Z.-H. (2012). Ensemble Methods: Foundations and Algorithms. CRC Press.
4. Aggarwal, C. C. (2017). Outlier Analysis (2nd ed.). Springer.
5. Breunig, M. M., Kriegel, H.-P., Ng, R. T., & Sander, J. (2000). LOF: Identifying density-based local outliers. ACM SIGMOD Record, 29(2), 93–104.
6. Pedregosa, F., Varoquaux, G., Gramfort, A., et al. (2011). Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12, 2825–2830.
7. Chalapathy, R., & Chawla, S. (2019). Deep Learning for Anomaly Detection: A Survey. arXiv:1901.03407.
8. Emmott, A., Das, S., Dietterich, T. G., Fern, A., & Wong, W.-K. (2016). A Meta-Analysis of the Anomaly Detection Problem. arXiv:1503.01158.
9. Bandaragoda, T., Ting, K. M., Albrecht, D., Liu, F. T., & Wells, J. R. (2014). Efficient anomaly detection by isolation using nearest neighbours. 2014 IEEE ICDM Workshop, 698–705.
10. Goldstein, M., & Uchida, S. (2016). A Comparative Evaluation of Unsupervised Anomaly Detection Algorithms for Multivariate Data. PLoS ONE, 11(4), e0152173.