Day 7 — Boxplots, IQR, and Tukey Fences 🧮📦

Spotting outliers with boxplots and robust fences! 📊

💡 Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.

🎯 Introduction

Boxplots provide a simple visual way to identify outliers using the IQR (Interquartile Range) and Tukey fences. This method is robust, doesn't assume normality, and works well with skewed or heavy-tailed data.

TL;DR:

Boxplots are the simplest visual way to spot outliers.

They rely on the IQR (Interquartile Range) — the middle 50% of your data — and build "fences" around it:

🧱

IQR = Q₃ − Q₁

Lower Fence = Q₁ − 1.5 × IQR

Upper Fence = Q₃ + 1.5 × IQR

Points outside these fences are suspected outliers.

It's simple, robust, and doesn't assume your data are Normal. ✅

🎯 The Goal

Find a rule-of-thumb for outliers that:

• Doesn't rely on the mean/SD (which break with extremes),
• Works on skewed or heavy-tailed data,
• Is visual, explainable, and easy to compute.

Enter: Tukey fences, the engine behind every boxplot. 💡

📦 The Anatomy of a Boxplot

Think of your dataset as a landscape:

• The box = the middle 50% (Q₁ → Q₃).
• The line inside = the median (Q₂).
• The whiskers = data within the fences.
• The dots outside = outliers.

Here's the anatomy in plain terms:

     *       *        <- Outliers
 |-------------------|  <- Fences
     |-----------|       <- Box (Q1–Q3)
         |               <- Median

🧩 The IQR measures the width of the box — how spread the middle half is.

• Larger IQR → more variability.
• Smaller IQR → tight clustering.

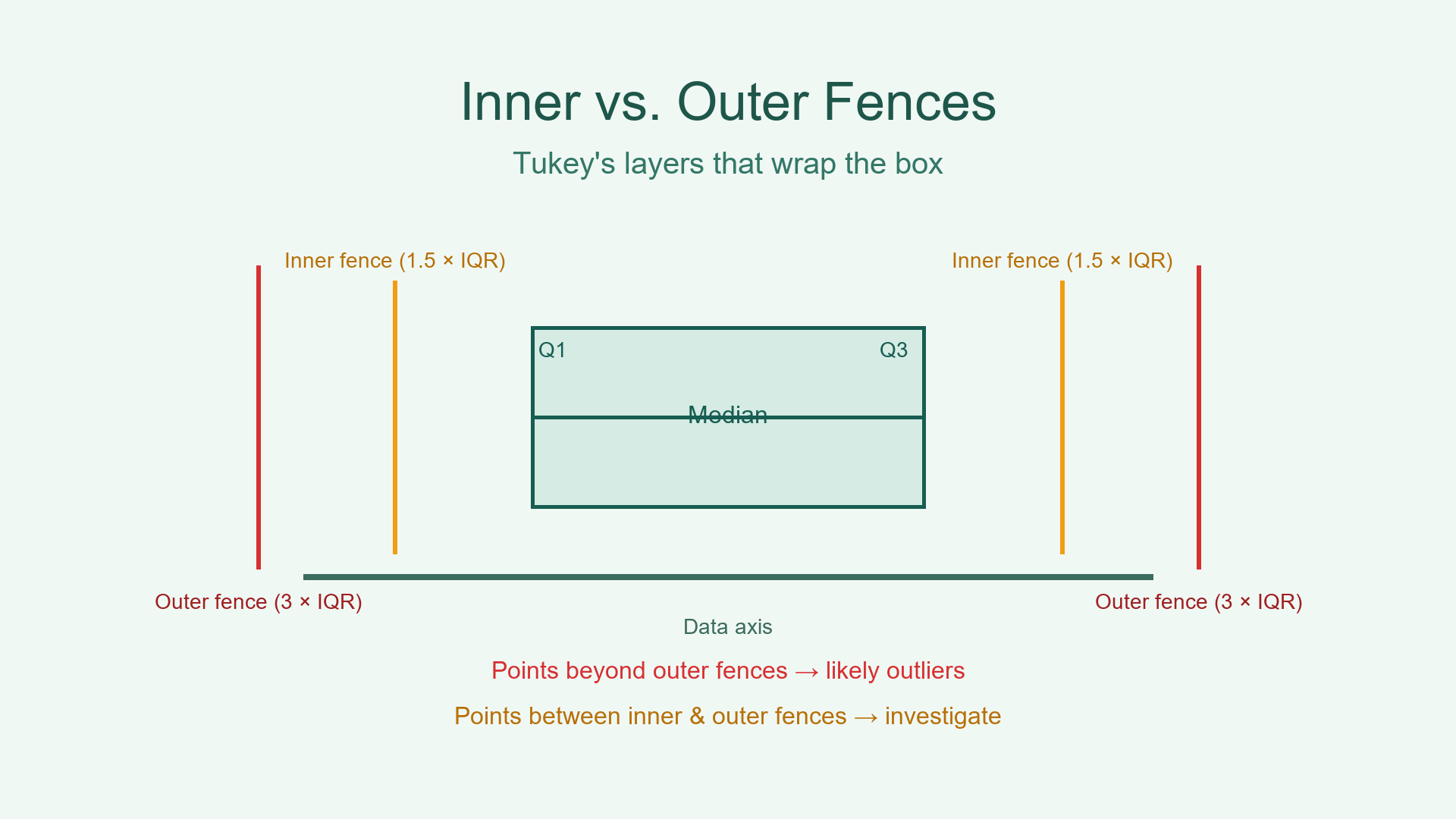
Tukey's inner and outer fences wrap the box to flag suspicious points.

🧮 Step-by-Step Example

Let's take this simple dataset:

[3, 4, 5, 6, 7, 8, 9, 15, 30]

1️⃣ Sort it (already sorted).

2️⃣ Find quartiles:

• Q₁ = lower 25th percentile = 4.5
• Q₂ = median = 7
• Q₃ = upper 75th percentile = 9

3️⃣ Compute IQR:

IQR = Q₃ − Q₁ = 9 − 4.5 = 4.5

4️⃣ Compute Tukey fences:

• Lower fence = Q₁ − 1.5 × IQR = 4.5 − 6.75 = −2.25
• Upper fence = Q₃ + 1.5 × IQR = 9 + 6.75 = 15.75

5️⃣ Flag outliers:

Any x < −2.25 or x > 15.75 is an outlier.

✅ Here, 30 > 15.75, so 30 is an outlier.

💡 That's it!

You've just built a nonparametric outlier detector — no mean, no SD, no assumptions.

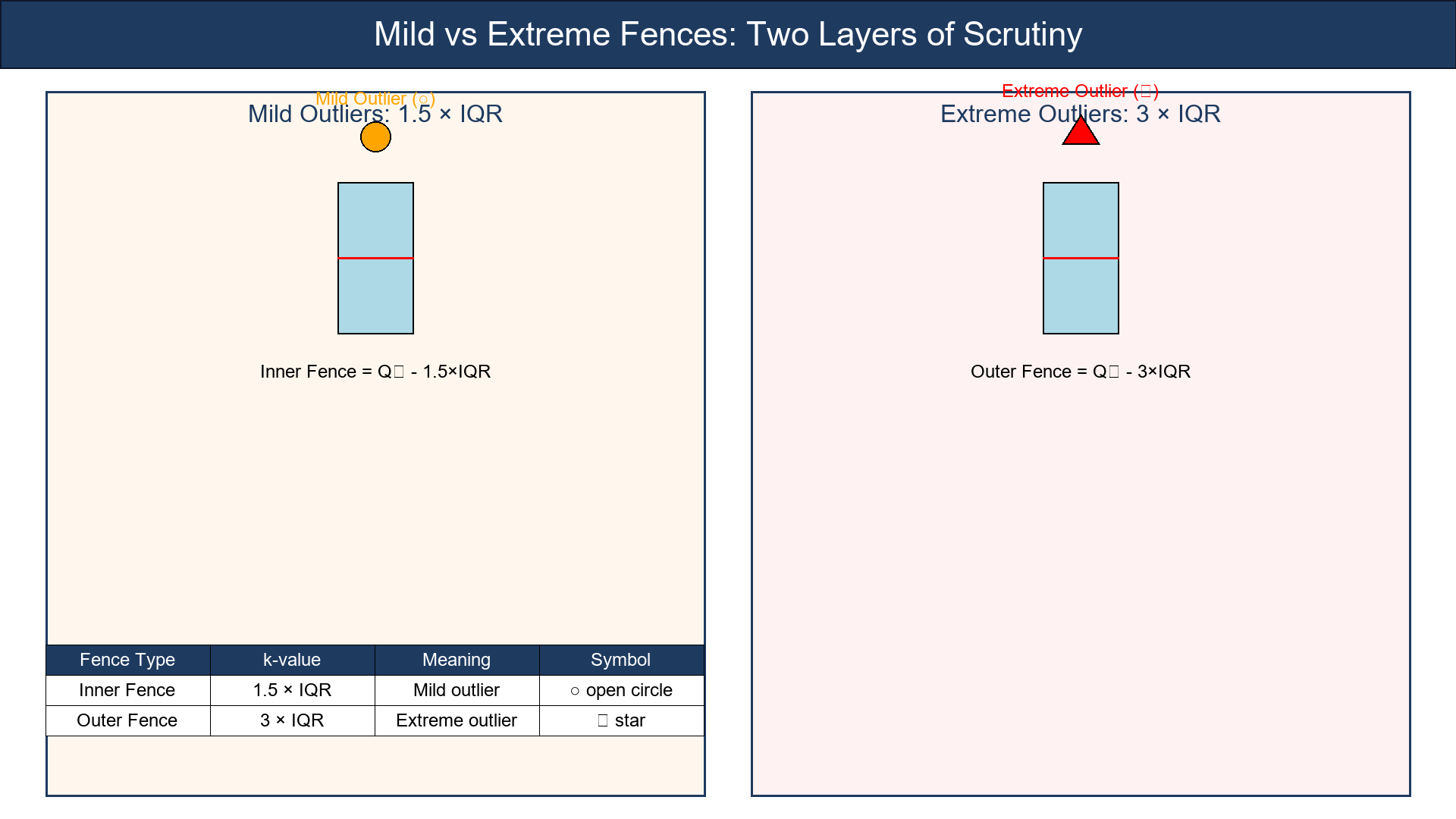
📏 Variants: Mild vs. Extreme Fences

Tukey suggested two layers of scrutiny:

| Fence Type | k-value | Meaning | Typical Symbol | |------------|---------|---------|----------------| | Inner Fence | 1.5 × IQR | Mild outlier | ○ open circle | | Outer Fence | 3 × IQR | Extreme outlier | ★ star |

This gives you nuance — not every far-off point is a villain; some are just adventurous. 😉

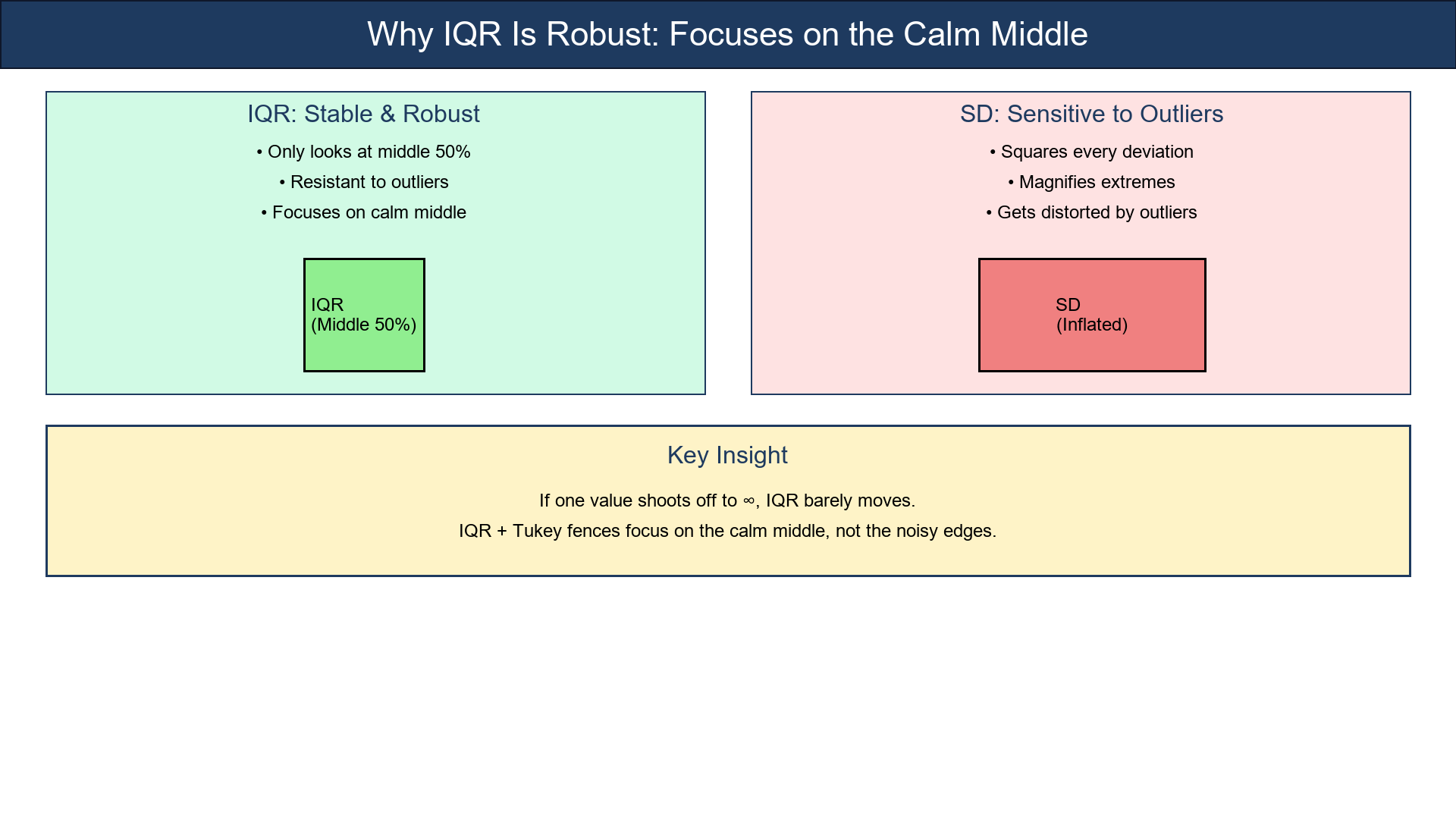
🧱 Why IQR Is Robust

Unlike the standard deviation, which squares every deviation (magnifying extremes), the IQR only looks at the middle 50%.

So if one value shoots off to ∞, IQR barely moves.

That's why the IQR + Tukey fences are robust — they focus on the calm middle, not the noisy edges.

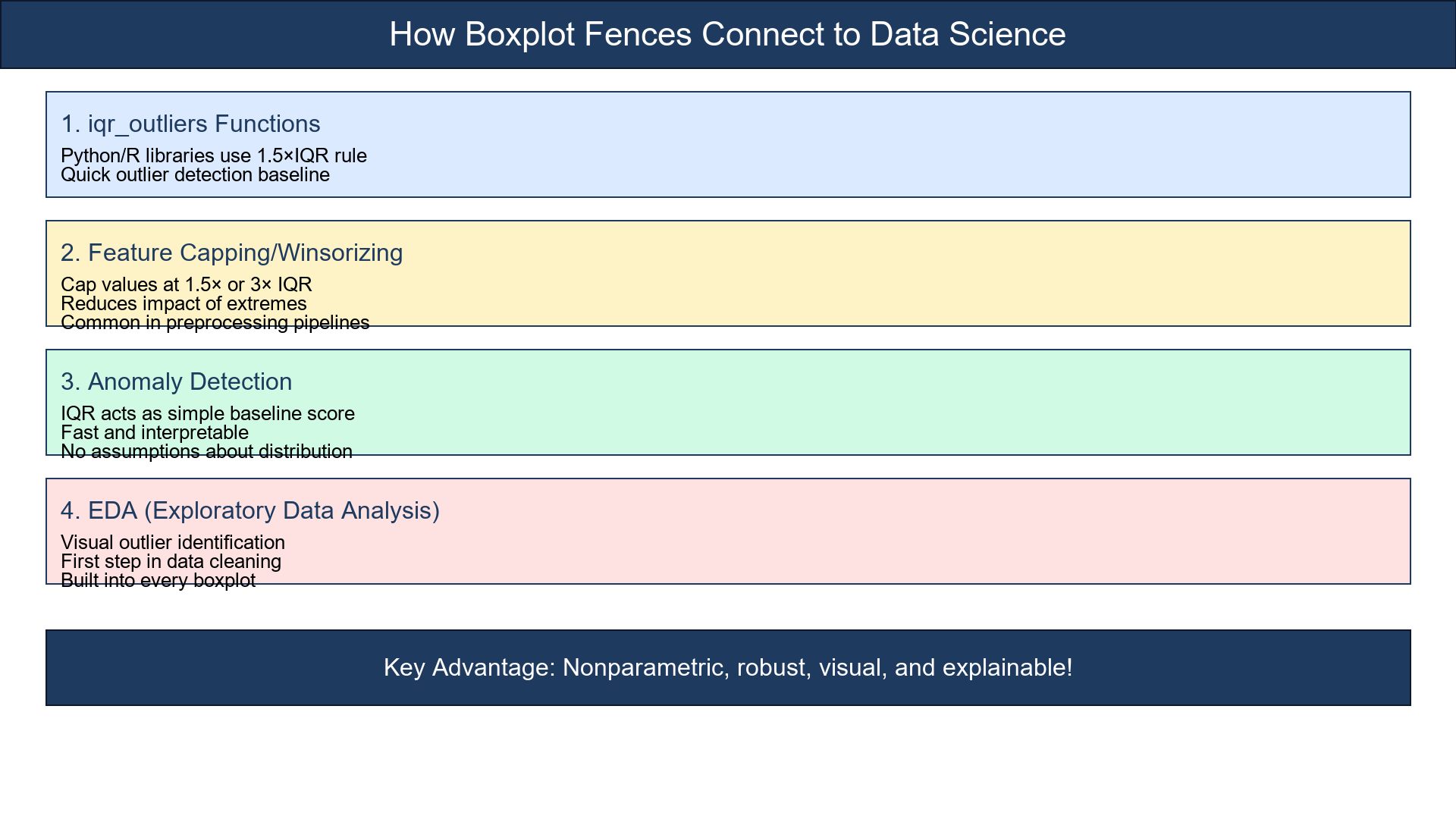
⚙️ How It Connects to Data Science

Boxplot fences are the conceptual ancestor of many robust methods:

• iqr_outliers functions in Python/R use the same fence logic.
• Feature capping/winsorizing often uses 1.5× or 3× IQR rules.
• In anomaly detection, IQR acts as a simple yet reliable baseline score.

In short: if you've drawn a boxplot, you've already done outlier detection! ✨

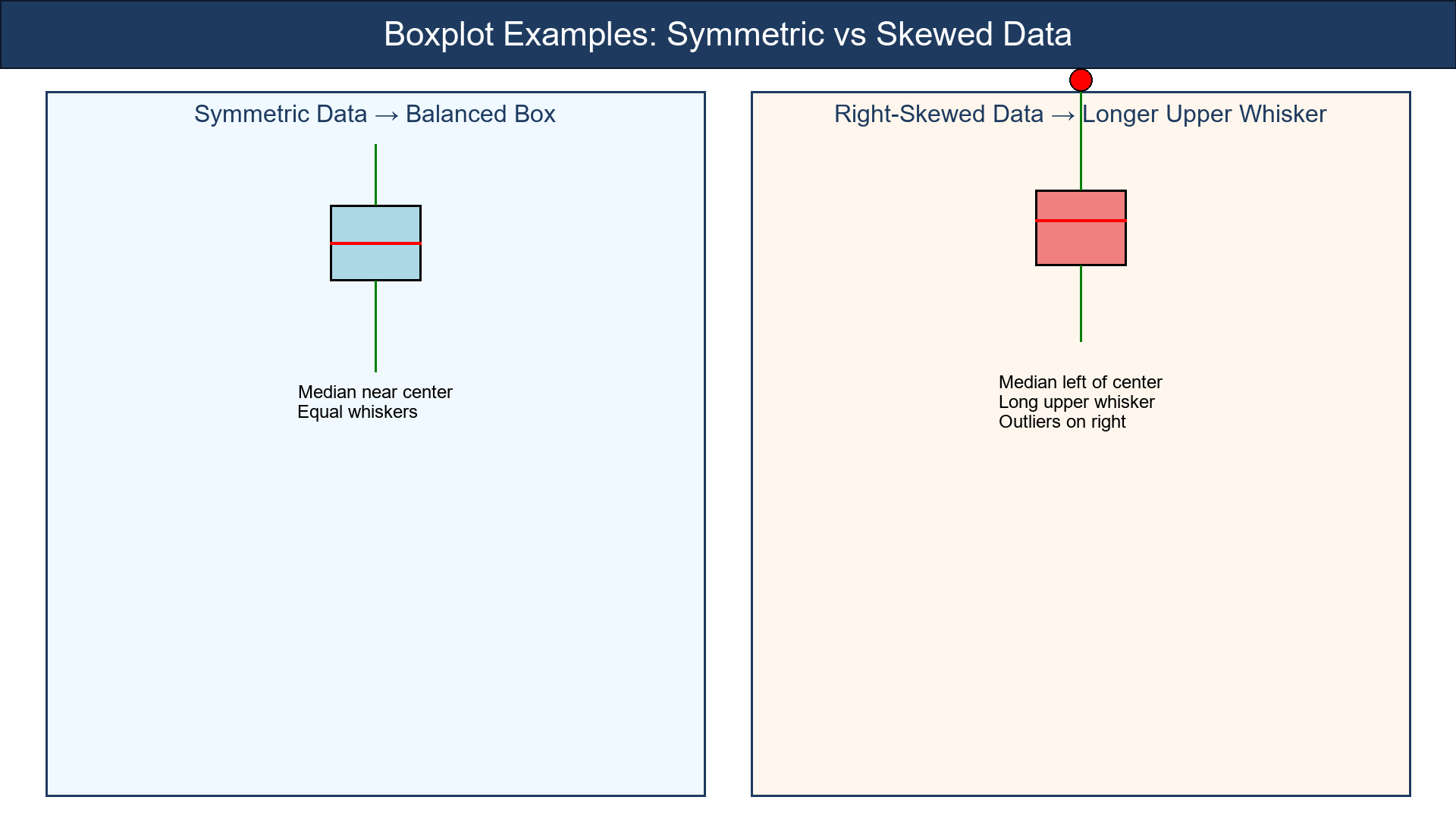
📈 Visual Idea

Show a clean boxplot with labeled parts:

• Median line
• Box edges (Q₁ & Q₃)
• Whiskers (fences)
• Dots for outliers

Use two examples:

1️⃣ Symmetric data → balanced box

2️⃣ Right-skewed data → longer upper whisker

🧠 Try It Yourself — Mini Exercise

Dataset:

[5, 7, 8, 9, 10, 10, 11, 12, 14, 25]

1️⃣ Find Q₁, Q₂, Q₃ and IQR.

2️⃣ Compute the fences for k = 1.5 and 3.

3️⃣ Which points fall outside each?

(Hint: 25 might raise some eyebrows 👀)

🌟 Takeaway

• Boxplots = a picture of the middle + the fences around it.
• IQR = robust measure of spread.
• Tukey fences = simple, nonparametric outlier rule.
• Visual + mathematical + explainable = the perfect first step in outlier analysis.

Boxplots don't just summarize data — they protect you from its surprises. 📦✨

📚 References

1. Tukey, J. W. (1977). Exploratory Data Analysis. Addison-Wesley.

2. Hoaglin, D. C., Mosteller, F., & Tukey, J. W. (Eds.). (1983). Understanding Robust and Exploratory Data Analysis. John Wiley & Sons.

3. McGill, R., Tukey, J. W., & Larsen, W. A. (1978). Variations of box plots. The American Statistician, 32(1), 12-16.

4. Frigge, M., Hoaglin, D. C., & Iglewicz, B. (1989). Some implementations of the boxplot. The American Statistician, 43(1), 50-54.

5. Tukey, J. W. (1962). The future of data analysis. Annals of Mathematical Statistics, 33(1), 1-67.

6. Mosteller, F., & Tukey, J. W. (1977). Data Analysis and Regression: A Second Course in Statistics. Addison-Wesley.

7. Rousseeuw, P. J., & Croux, C. (1993). Alternatives to the median absolute deviation. Journal of the American Statistical Association, 88(424), 1273-1283.

8. Hubert, M., & Van der Veeken, S. (2008). Outlier detection for skewed data. Journal of Chemometrics, 22(3-4), 235-246.

9. Leys, C., Ley, C., Klein, O., Bernard, P., & Licata, L. (2013). Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. Journal of Experimental Social Psychology, 49(4), 764-766.

10. Barnett, V., & Lewis, T. (1994). Outliers in Statistical Data (3rd ed.). John Wiley & Sons.