Day 12 — Binning and Deciles: Taming Continuous Chaos 📊🗂️

Every data point tells a story; binning organizes them into meaningful chapters.

Binning transforms continuous variables into categorical groups, making patterns visible and analysis manageable.

💡 Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.

😵 The Overwhelm Problem: Too Many Numbers!

Imagine you're analyzing customer ages and income to predict product effectiveness:

Raw Data (100 customers):

Age: 23.4, 45.7, 31.2, 52.8, 38.9, 41.3, 29.7, ...

Income: $43,200, $87,500, $52,300, $91,800, ...

Question: How does effectiveness vary by age and income? 🤔

Problem: With 100 unique ages and 100 unique incomes, you have 100 × 100 = 10,000 possible combinations! You can't make sense of this! 🤯

Solution: BINNING! Group continuous values into meaningful buckets. 🗑️✨

🎯 What is Binning?

Binning (also called discretization) means converting continuous numbers into categorical groups.

Visual Transformation

Before (Continuous):

Ages: 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, ...

      ↓  ↓  ↓  ↓  ↓  ↓  ↓  ↓  ↓  ↓

      Too many individual values!

After (Binned):

Age Groups: [18-30], [31-40], [41-50], [51-60], [61+]

            Young   Young    Middle   Middle   Senior

                    Adult    Age      Age

Benefits:

✅ Easier to understand ("30s vs 40s")

✅ Reveals patterns ("effectiveness higher in 40s")

✅ Reduces noise (smooths out random variation)

✅ Creates interpretable tables and charts

📏 Types of Binning

1. Equal-Width Binning (Fixed Intervals)

Divide the range into bins of equal size.

Example: Ages from 20 to 80

Bin 1: [20-30)  ← 10 years wide

Bin 2: [30-40)  ← 10 years wide

Bin 3: [40-50)  ← 10 years wide

Bin 4: [50-60)  ← 10 years wide

Bin 5: [60-70)  ← 10 years wide

Bin 6: [70-80]  ← 10 years wide

Formula:

Bin width = (max - min) / number_of_bins

Bin edges = [min, min + width, min + 2×width, ..., max]

Pros:

• Simple, intuitive

• Equal-sized ranges

Cons:

• Bins can have very different counts

• Sensitive to outliers (one extreme value stretches everything)

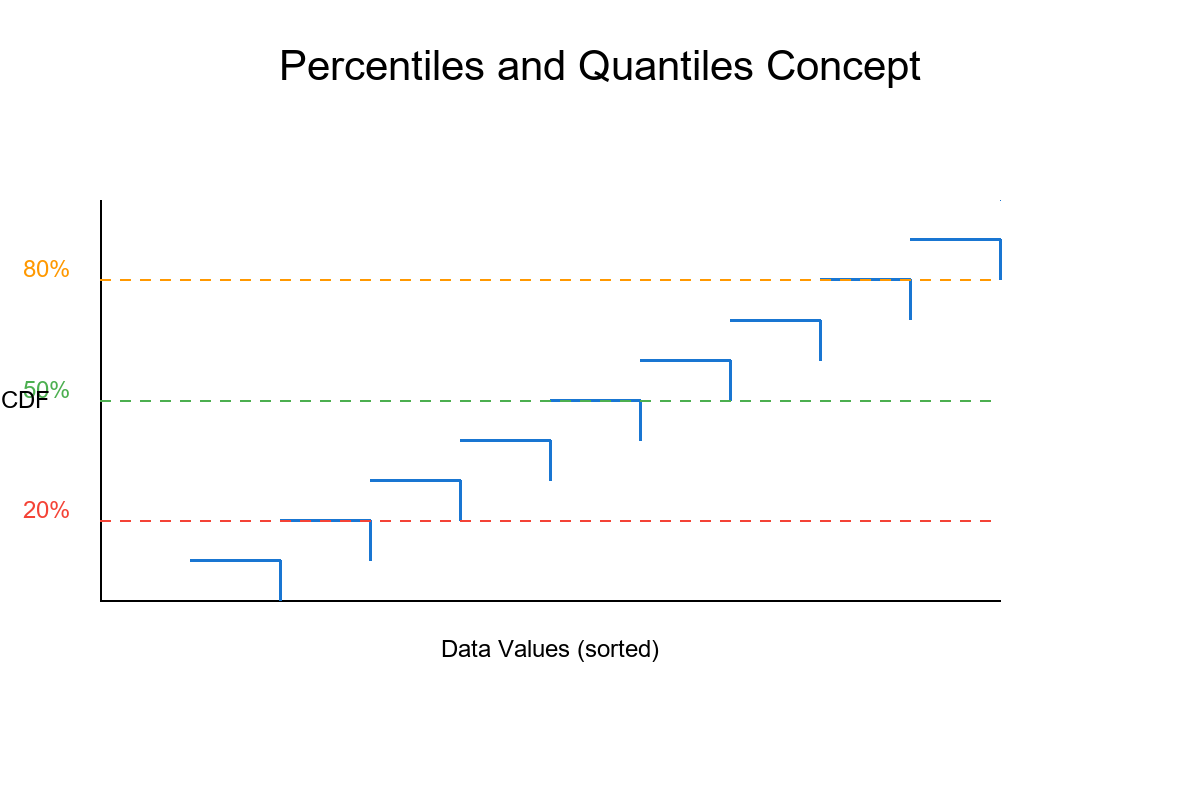
2. Equal-Frequency Binning (Quantiles/Deciles) ⚖️

Divide data so each bin has approximately the same number of observations.

Example: 100 ages, want 5 bins

Bin 1: [20-28]  ← 20 people

Bin 2: [29-35]  ← 20 people

Bin 3: [36-42]  ← 20 people

Bin 4: [43-52]  ← 20 people

Bin 5: [53-80]  ← 20 people

Notice: Bin widths vary, but counts are equal!

Special Cases:

• Quartiles: 4 bins (25% each) - Q₁, Q₂, Q₃, Q₄

• Quintiles: 5 bins (20% each)

• Deciles: 10 bins (10% each) ⭐ Most common!

• Percentiles: 100 bins (1% each)

Pros:

• Each bin has enough data for reliable statistics

• Not affected by outliers

• Great for comparing "top 10%" vs "bottom 10%"

Cons:

• Bin widths can be confusing (why is one bin 5 years and another 15?)

• Ties can make exact equal frequencies impossible

3. Custom Binning (Domain-Driven) 🎨

Create bins based on real-world meaning.

Example: Credit scores

[300-579]: Poor

[580-669]: Fair

[670-739]: Good

[740-799]: Very Good

[800-850]: Excellent

Example: Age groups

[0-12]:   Child

[13-17]:  Teen

[18-25]:  Young Adult

[26-40]:  Adult

[41-60]:  Middle Age

[61+]:    Senior

Pros:

• Makes business sense

• Easy to communicate

• Aligns with existing categories

Cons:

• Requires domain expertise

• May not have equal counts

⭐ Deciles: The Star of the Show

Deciles divide your data into 10 equal-frequency bins, each containing 10% of observations.

Why Deciles? 🤔

1. Balance: Enough bins to see patterns, not so many you lose interpretability

2. Statistical Power: Each bin has ≥10% of data (reliable estimates)

3. Industry Standard: Used in credit scoring, risk modeling, marketing

4. Percentile Friendly: Decile 10 = top 10%, easy to explain!

The Math Behind Deciles 🧮

For n observations, sorted from smallest to largest:

Decile 1: Observations 1 to n/10        (0-10th percentile)

Decile 2: Observations n/10 to 2n/10    (10-20th percentile)

Decile 3: Observations 2n/10 to 3n/10   (20-30th percentile)

...

Decile 10: Observations 9n/10 to n      (90-100th percentile)

Decile boundaries (cut points):

D₁ = 10th percentile

D₂ = 20th percentile

D₃ = 30th percentile

...

D₉ = 90th percentile

Example Calculation 📐

Data: [10, 15, 18, 22, 25, 30, 35, 40, 50, 60] (n=10)

Want: Deciles (10 bins, 1 obs each ideally)

Step 1: Already sorted ✅

Step 2: Calculate decile positions

Position for k-th decile = k × (n+1) / 10

D₁ position = 1 × 11/10 = 1.1 → between 1st and 2nd obs

D₂ position = 2 × 11/10 = 2.2 → between 2nd and 3rd obs

...

Step 3: Interpolate if needed

D₁ = 10 + 0.1×(15-10) = 10.5

D₂ = 15 + 0.2×(18-15) = 15.6

D₃ = 18 + 0.3×(22-18) = 19.2

...

Step 4: Assign observations to deciles

Decile 1: [10]        (≤10.5)

Decile 2: [15]        (10.5-15.6)

Decile 3: [18]        (15.6-19.2)

Decile 4: [22]        (19.2-23.4)

Decile 5: [25]        (23.4-27.5)

Decile 6: [30]        (27.5-32.5)

Decile 7: [35]        (32.5-37.5)

Decile 8: [40]        (37.5-45.0)

Decile 9: [50]        (45.0-55.0)

Decile 10: [60]       (>55.0)

Each decile has exactly 1 observation! ⚖️

🎓 Exercise: Proving Deciles Equalize Counts

Claim: In the ideal case (no ties), each decile contains exactly n/10 observations.

Proof:

Setup:

• n observations: x₁, x₂, ..., xₙ (sorted)

• All values distinct (no ties)

• Want to divide into 10 bins of equal size

Method:

1. Calculate decile boundaries at percentiles: 10, 20, 30, ..., 90

2. Each boundary falls at position k×n/10 for k=1,2,...,9

Observation count per decile:

Decile 1: Positions 1 to n/10           → n/10 observations

Decile 2: Positions n/10+1 to 2n/10     → n/10 observations

Decile 3: Positions 2n/10+1 to 3n/10    → n/10 observations

...

Decile 10: Positions 9n/10+1 to n       → n/10 observations

Total check:

Sum = 10 × (n/10) = n ✅

All observations accounted for!

Example with n=100:

Decile 1: Obs 1-10     → 10 obs

Decile 2: Obs 11-20    → 10 obs

Decile 3: Obs 21-30    → 10 obs

...

Decile 10: Obs 91-100  → 10 obs

Total = 10×10 = 100 ✅

What About Ties? 🤝

Problem: If multiple observations have the same value, decile boundaries may fall "in the middle" of a tie group.

Example:

Data: [10, 20, 20, 20, 20, 30, 40, 50, 60, 70]

             ↑________↑

             Tied values

Want decile 2 boundary at 20th percentile (position 2)

But positions 2, 3, 4, 5 all equal 20!

Solutions:

1. Lower boundary: Put tied values in lower decile

   • Decile 1: [10, 20, 20, 20, 20] → 5 obs

   • Decile 2: [30] → 1 obs

   • Result: Unequal counts 😕

2. Upper boundary: Put tied values in upper decile

   • Decile 1: [10] → 1 obs

   • Decile 2: [20, 20, 20, 20, 30] → 5 obs

   • Result: Still unequal 😕

3. Random assignment: Randomly assign tied values

   • Decile 1: [10, 20, 20] → 3 obs (random)

   • Decile 2: [20, 20, 30] → 3 obs (random)

   • Result: Non-deterministic 🎲

4. Accept it: Ties cause slight imbalance, that's life! 🤷‍♂️

   • Document the issue

   • Usually not a big deal in practice

In practice: Most statistical software uses method 4 (accept slight imbalance). With large datasets and continuous variables, ties are rare anyway!

💪 Contingency Tables (Cross-Tabs): The Power Duo

Once you bin two variables, you can create a contingency table (also called cross-tab) showing how they interact.

Setup

Variables:

• Age (binned into 5 groups)

• Income (binned into 5 groups)

• Outcome: Effective (Yes/No)

Simple Frequency Table 📊

Question: How many people in each age group?

Age Group    | Count | Percent

-------------|-------|--------

18-30        |   25  |  25%

31-40        |   30  |  30%

41-50        |   20  |  20%

51-60        |   15  |  15%

61+          |   10  |  10%

-------------|-------|--------

Total        |  100  | 100%

Code:

import pandas as pd

# Create bins
age_bins = [18, 30, 40, 50, 60, 100]
age_labels = ['18-30', '31-40', '41-50', '51-60', '61+']
df['age_group'] = pd.cut(df['age'], bins=age_bins, labels=age_labels)

# Frequency table
frequency_table = df['age_group'].value_counts().sort_index()
print(frequency_table)

Cross-Tab: Two Variables 🔀

Question: How does effectiveness vary by age AND income?

                Income Group

              Low    Medium   High

Age    18-30   12      8       5     (25 total)

Group  31-40   10     12       8     (30 total)

       41-50    6      8       6     (20 total)

       51-60    4      7       4     (15 total)

       61+      3      4       3     (10 total)

       

Column Total   35     39      26    (100 total)

Interpretation:

• Young people spread across income levels

• Middle-aged concentrated in medium income

• Seniors fewer overall

Code:

# Create income bins
income_bins = [0, 40000, 70000, 150000]
income_labels = ['Low', 'Medium', 'High']
df['income_group'] = pd.cut(df['income'], bins=income_bins, labels=income_labels)

# Cross-tab
crosstab = pd.crosstab(df['age_group'], df['income_group'])
print(crosstab)

🎯 Per-Bin Rate Estimates: Finding the Signal

The real power comes when we calculate rates (percentages) within each bin.

Setup

Goal: Calculate "Percent Effective" for each age-income combination

Formula:

Percent Effective in bin = (# Effective in bin / Total in bin) × 100%

Example Calculation

Age 18-30, Income Low:

• Total in bin: 12 people

• Effective: 8 people

• Percent Effective: 8/12 = 66.7% ✨

Age 51-60, Income High:

• Total in bin: 4 people

• Effective: 3 people

• Percent Effective: 3/4 = 75.0% 🎉

Full Cross-Tab with Rates 📈

Percent Effective by Age and Income

                Income Group

              Low      Medium    High

Age    18-30  66.7%    62.5%    60.0%

Group  31-40  70.0%    75.0%    87.5%  ← Peak!

       41-50  66.7%    75.0%    83.3%

       51-60  50.0%    71.4%    75.0%

       61+    33.3%    50.0%    66.7%

Insight: Effectiveness peaks for 31-40 age group 

         with high income! 🎯

Code:

# Add effectiveness column (0 or 1)
df['effective'] = df['outcome'].map({'Yes': 1, 'No': 0})

# Calculate rates
rate_table = df.groupby(['age_group', 'income_group'])['effective'].agg([
    ('count', 'size'),
    ('effective_count', 'sum'),
    ('percent_effective', lambda x: x.mean() * 100)
])

print(rate_table)

🔥 Heatmaps: The Visual Payoff

Heatmaps turn cross-tabs into beautiful, intuitive visuals.

Count Heatmap 🟦

Shows how many observations in each cell.

        Income

        Low  Med  High

Age 30   🟦  🟦   🟦    (12, 8, 5)

    40   🟦  🟦   🟦    (10, 12, 8)

    50   🟨  🟦   🟨    (6, 8, 6)

    60   🟨  🟨   🟨    (4, 7, 4)

    70   🟨  🟨   🟨    (3, 4, 3)

    🟦 = Many observations (>8)

    🟨 = Few observations (<6)

Insight: Data concentrated in younger age groups. 📊

Percent Effective Heatmap 🔥

Shows effectiveness rate in each cell.

        Income

        Low   Med   High

Age 30  67%   63%   60%    🟨

    40  70%   75%   88%    🟥 ← Hotspot!

    50  67%   75%   83%    🟧

    60  50%   71%   75%    🟧

    70  33%   50%   67%    🟨

    🟥 = High effectiveness (>80%)

    🟧 = Medium (65-80%)

    🟨 = Low (<65%)

Insight: Target 31-40 age group with high income for best results! 🎯

Code:

import seaborn as sns
import matplotlib.pyplot as plt

# Pivot for heatmap
heatmap_data = rate_table['percent_effective'].unstack()

# Create heatmap
plt.figure(figsize=(8, 6))
sns.heatmap(heatmap_data, annot=True, fmt='.1f', cmap='RdYlGn', 
            cbar_kws={'label': 'Percent Effective'})
plt.title('Treatment Effectiveness by Age and Income')
plt.xlabel('Income Group')
plt.ylabel('Age Group')
plt.tight_layout()
plt.show()

🔧 Tie-Back: get_cross_tab in Our Toolkit

def get_cross_tab(df, row_var, col_var, value_var, 
                  row_bins=None, col_bins=None, aggfunc='mean'):
    """
    Create cross-tab with optional binning
    
    Parameters:
    - df: DataFrame
    - row_var: Variable for rows (will be binned if row_bins provided)
    - col_var: Variable for columns (will be binned if col_bins provided)
    - value_var: Variable to aggregate (e.g., 'effective')
    - row_bins: Number of bins or list of bin edges for rows
    - col_bins: Number of bins or list of bin edges for columns
    - aggfunc: Aggregation function ('mean', 'sum', 'count')
    
    Returns: 
    - crosstab: Pivot table
    - heatmap: matplotlib figure
    """
    df_copy = df.copy()
    
    # Bin row variable if needed
    if row_bins is not None:
        if isinstance(row_bins, int):
            # Use quantile bins (deciles, quartiles, etc.)
            df_copy[f'{row_var}_binned'] = pd.qcut(
                df[row_var], q=row_bins, labels=False, duplicates='drop'
            )
        else:
            # Use custom bin edges
            df_copy[f'{row_var}_binned'] = pd.cut(
                df[row_var], bins=row_bins
            )
        row_var = f'{row_var}_binned'
    
    # Bin column variable if needed
    if col_bins is not None:
        if isinstance(col_bins, int):
            df_copy[f'{col_var}_binned'] = pd.qcut(
                df[col_var], q=col_bins, labels=False, duplicates='drop'
            )
        else:
            df_copy[f'{col_var}_binned'] = pd.cut(
                df[col_var], bins=col_bins
            )
        col_var = f'{col_var}_binned'
    
    # Create cross-tab
    if aggfunc == 'mean':
        crosstab = df_copy.pivot_table(
            values=value_var, 
            index=row_var, 
            columns=col_var, 
            aggfunc='mean'
        ) * 100  # Convert to percentage
        title = f'Percent {value_var.title()}'
    elif aggfunc == 'count':
        crosstab = pd.crosstab(df_copy[row_var], df_copy[col_var])
        title = 'Count'
    else:
        crosstab = df_copy.pivot_table(
            values=value_var, 
            index=row_var, 
            columns=col_var, 
            aggfunc=aggfunc
        )
        title = f'{aggfunc.title()} of {value_var.title()}'
    
    # Create heatmap
    fig, ax = plt.subplots(figsize=(10, 6))
    sns.heatmap(crosstab, annot=True, fmt='.1f', cmap='RdYlGn', 
                ax=ax, cbar_kws={'label': title})
    ax.set_title(f'{title} by {row_var.title()} and {col_var.title()}')
    ax.set_xlabel(col_var.title())
    ax.set_ylabel(row_var.title())
    plt.tight_layout()
    
    return crosstab, fig

Usage:

# Example 1: Deciles (10 bins each)
crosstab, fig = get_cross_tab(
    df, 
    row_var='age', 
    col_var='income',
    value_var='effective',
    row_bins=10,  # Age deciles
    col_bins=10,  # Income deciles
    aggfunc='mean'
)

# Example 2: Custom bins
age_bins = [18, 30, 40, 50, 60, 100]
income_bins = [0, 40000, 70000, 150000]
crosstab, fig = get_cross_tab(
    df,
    row_var='age',
    col_var='income', 
    value_var='effective',
    row_bins=age_bins,
    col_bins=income_bins,
    aggfunc='mean'
)

⚠️ Common Pitfalls and Best Practices

Pitfall 1: Too Many Bins 🚫

Problem:

10 age bins × 10 income bins = 100 cells

With 100 observations, average 1 per cell!

Rates unreliable, heatmap noisy.

Solution: Use 3-5 bins per variable (max 25 cells total)

Pitfall 2: Too Few Bins 🚫

Problem:

2 age bins × 2 income bins = 4 cells

Loses all nuance, everything averaged out!

Solution: At least 3 bins per variable to see patterns

Pitfall 3: Unequal Sample Sizes 🚫

Problem:

Cell A: 50 obs, 40% effective (reliable ✅)

Cell B: 2 obs, 100% effective (luck! ❌)

Solution:

• Report sample sizes alongside rates

• Use confidence intervals for small cells

• Consider merging small bins

Pitfall 4: Ignoring Statistical Significance 🚫

Problem:

Age 18-30: 60% effective

Age 31-40: 65% effective

Is 5% difference real or random?

Solution: Use chi-square test or proportion tests

Code:

from scipy.stats import chi2_contingency

# Test if age and effectiveness are independent
contingency_table = pd.crosstab(df['age_group'], df['effective'])
chi2, p_value, dof, expected = chi2_contingency(contingency_table)

if p_value < 0.05:
    print("Relationship is statistically significant!")
else:
    print("Could be random chance.")

✅ Best Practices

1. Start with Deciles 📊

• Industry standard

• Good balance of detail and interpretability

• Each bin has 10% of data (reliable stats)

2. Check Sample Sizes 🔍

Always show counts alongside rates:

Age 31-40, High Income: 87.5% effective (n=8)

                                         ↑

                        Don't ignore this!

3. Use Color Wisely 🎨

• Green → Good (high effectiveness)

• Red → Bad (low effectiveness)

• Avoid rainbow (hard to interpret)

4. Label Clearly 🏷️

Good: "Percent Effective by Age Decile and Income Quartile"

Bad:  "Heatmap"

5. Document Bin Choices 📝

# Document your binning
"""
Age bins: Deciles (10% each)

Income bins: Quartiles (25% each)

Rationale: Age has wider range, needs more granularity
"""

6. Validate Patterns ✅

• Does the pattern make sense?

• Age 31-40 most effective? Check if that age group is healthiest, most compliant, etc.

• Don't just report numbers, explain them!

🎯 When to Use Binning

Perfect For:

✅ Exploratory Analysis: "Where are the patterns?"

✅ Communication: Easier than scatter plots for stakeholders

✅ Risk Modeling: Credit scores, insurance premiums

✅ A/B Testing: Segment analysis (young vs old users)

✅ Feature Engineering: Convert continuous → categorical for tree models

Don't Use When:

❌ Sample size too small (n < 50): Bins will be unreliable

❌ Relationships are smooth/linear: Binning loses information

❌ Need exact predictions: Binning discretizes, loses precision

❌ Variables naturally categorical: No need to bin "Country" or "Gender"

🎯 Summary

Binning transforms overwhelming continuous data into digestible insights:

Key Concepts:

✅ Equal-width bins: Fixed intervals (simple but sensitive to outliers)

✅ Equal-frequency bins (deciles): Same count per bin (robust, fair)

✅ Deciles specifically: 10 bins, 10% each - the gold standard ⭐

✅ Contingency tables: Cross-tabs show interaction between two binned variables

✅ Per-bin rates: Calculate percentages within each cell

✅ Heatmaps: Visual representation of cross-tabs (color = value)

✅ Ties: Can make perfect equal-frequency binning impossible (accept slight imbalance)

The Decile Proof:

n observations ÷ 10 bins = n/10 per bin (when no ties)

Total = 10 × (n/10) = n ✅

Workflow:

1. Bin continuous variables (deciles usually best)

2. Cross-tab to see interactions

3. Calculate rates for the outcome of interest

4. Visualize with heatmaps

5. Interpret and make decisions

Real Impact:

📊 "Customers age 31-40 with high income have 87.5% satisfaction"

🎯 Much clearer than: "Satisfaction correlates with age (r=0.23, p=0.04)"

🌟 Takeaway

Binning transforms overwhelming continuous data into digestible, actionable insights. Master equal-width and equal-frequency binning, understand deciles (10 equal-frequency bins), and create powerful cross-tabs and heatmaps to reveal patterns in your data. When you have too many numbers to make sense of, binning is your organizing principle.

📚 References

1. Tukey, J. W. (1977). Exploratory Data Analysis. Addison-Wesley.

2. Freedman, D., Pisani, R., & Purves, R. (2007). Statistics (4th ed.). W. W. Norton & Company.

3. Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer.

4. Agresti, A. (2007). An Introduction to Categorical Data Analysis (2nd ed.). Wiley-Interscience.

5. Wickham, H., & Grolemund, G. (2017). R for Data Science: Import, Tidy, Transform, Visualize, and Model Data. O'Reilly Media.

6. McKinney, W. (2017). Python for Data Analysis: Data Wrangling with Pandas, NumPy, and IPython (2nd ed.). O'Reilly Media.

7. Gelman, A., & Hill, J. (2006). Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press.

8. Mosteller, F., & Tukey, J. W. (1977). Data Analysis and Regression: A Second Course in Statistics. Addison-Wesley.

9. Hoaglin, D. C., Mosteller, F., & Tukey, J. W. (Eds.). (2000). Understanding Robust and Exploratory Data Analysis. Wiley.

10. Cleveland, W. S. (1993). Visualizing Data. Hobart Press.

💡 Note: This article uses technical terms like binning, deciles, quantiles, contingency tables, cross-tabs, and heatmaps. For definitions, check out the Key Terms & Glossary page.