Day 17 — Robust Ratios and Division by Zero ⚖️🧮

Making ratios behave, even when denominators misbehave!

Robust ratios protect your calculations from division by zero and near-zero denominators, ensuring stable and reliable computations.

Ratios are powerful but dangerous—division by values near zero can make them explode! Learn how to design stable ratio features, guard against tiny denominators, and choose a principled epsilon using robust measures.

💡 Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.

The Ratio Problem 💥

Ratios are the bread and butter of data science:

Common examples:

Conversion rate = clicks / views
Efficiency = output / cost
Growth rate = (current - past) / past
Risk score = amount / avg_balance

But these simple formulas hide a sneaky trap—what happens when the denominator is 0 or nearly 0?

The problem:

Example	Computation	Result	Issue
	5 / 0	∞	Infinity \| Division by zero error 🚫
	5 / 0.00001	500,000	Huge number \| Explodes in scale 💥
💥	0 / 0	NaN	Undefined \| Not a number 😵

Real-world impact:

User with $0 balance → risk_score = amount / 0 → CRASH! 💥

Your models break in production, your dashboards show infinity, and your stakeholders lose trust.

The question: How do we make ratios safe and stable? 🎯

What is a Robust Ratio? 🛡️

Definition: A ratio that handles edge cases gracefully without exploding or crashing

Key principles:

Guard the denominator: Never divide by zero or near-zero values
Use principled epsilon: Choose stabilization constant based on data scale
Maintain continuity: Smooth transitions, not sudden jumps
Log and monitor: Track when guards are triggered

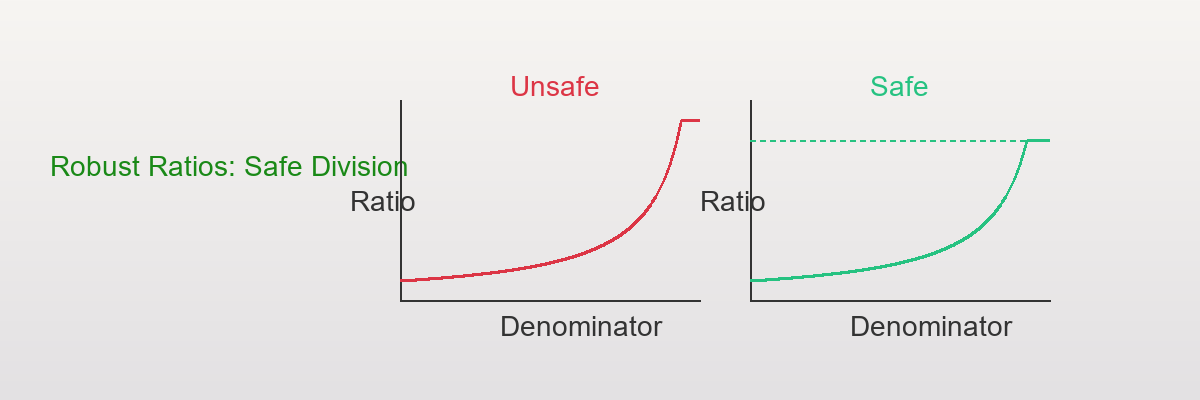
Visual intuition:

Show code (11 lines)

Unsafe ratio:     Safe ratio:
    ↑                  ↑
 | |
 |    ∞ |    ──────── (clipped)
 |   / |   /
 |  / |  /
 | / | /
 |/ |/
────┴───────────    ───┴───────────
  0  denominator      0  denominator

Before: Ratio explodes to infinity near zero

After: Ratio smoothly plateaus at a maximum value

Guarding denominators prevents division by zero errors, ensuring ratios remain stable and predictable even with edge cases.

The Core Solution: Guard the Denominator 🔒

Before dividing, always ask:

"Is my denominator safe enough to divide by?"

Basic pattern:

Show code (14 lines)

def safe_ratio(num, den, eps=1e-6):
    """
    Compute ratio with protection against small denominators
    
    Parameters:
    - num: numerator
    - den: denominator
    - eps: epsilon (small constant to replace near-zero denominators)
    
    Returns:
    - ratio: num / max(den, eps)
    """
    return num / np.where(np.abs(den) < eps, eps, den)

How it works:

Check if |den| < eps
If yes → replace with eps (small constant)
If no → use original den
Compute ratio normally

Example:

num = 5
den = [10, 2, 0.5, 0.05, 0.001, 0]
eps = 1e-6

ratios = safe_ratio(num, den, eps)
# Result: [0.5, 2.5, 10.0, 100.0, 5e6, 5e6]

Benefits:

✅ No division by zero errors
✅ Smooth, continuous behavior
✅ Predictable maximum values
✅ Production-safe

Why Use a Principled Epsilon? 📐

Problem with fixed epsilon:

Setting eps = 1e-6 or 1e-9 blindly can backfire:

# Bad: Fixed epsilon
eps = 1e-6  # Too small for large-scale data
ratio = num / max(den, eps)

# If den values are in millions:
# den = 1,000,000 → ratio works fine
# den = 0.000001 → ratio = 5e6 (explodes!)

Why it fails:

Arbitrary constant doesn't match data scale
Too small → still explodes
Too large → distorts real ratios
Doesn't adapt to data distribution

Solution: Data-driven epsilon

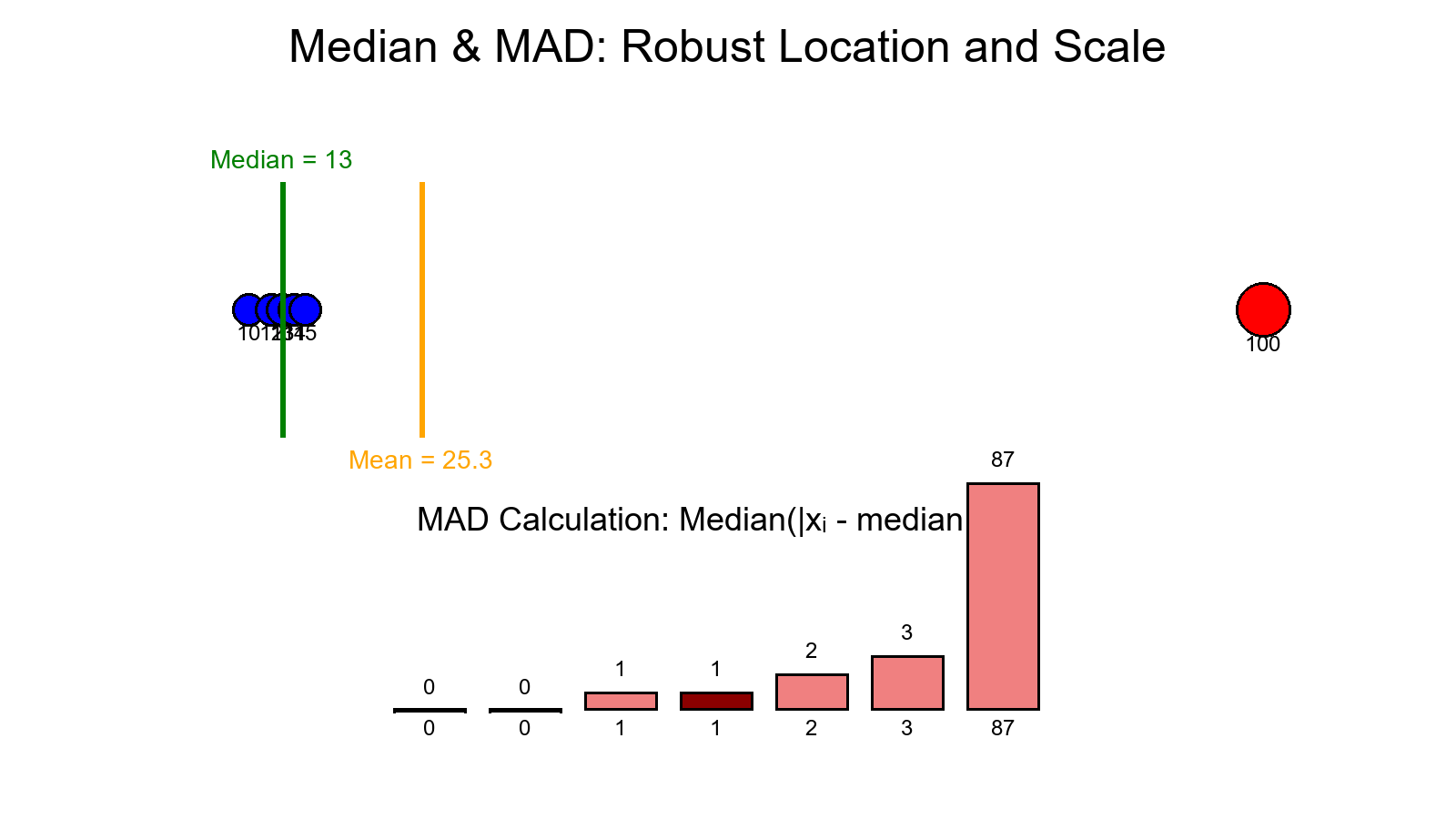
Make ε depend on your denominator's spread using robust measures.

Robust epsilon formula:

ε = c × MAD(denominator)

Where:

MAD = Median Absolute Deviation (robust measure of scale)
c = scaling factor (typically 0.1 to 0.5)

Why MAD?

Robust to outliers (unlike standard deviation)
Scale-invariant (adapts to data magnitude)
Interpretable (median-based, not mean-based)

Implementation:

Show code (21 lines)

def robust_epsilon(den, c=0.1):
    """
    Compute epsilon based on denominator's spread using MAD
    
    Parameters:
    - den: denominator values
    - c: scaling factor (default 0.1)
    
    Returns:
    - eps: data-driven epsilon
    """
    median_den = np.median(den)
    mad = np.median(np.abs(den - median_den))
    return c * mad

# Usage
denominator_data = [10, 2, 0.5, 0.05, 0.001, 0]
numerator_data = [5, 5, 5, 5, 5, 5]
eps = robust_epsilon(denominator_data, c=0.1)
ratio = safe_ratio(numerator_data, denominator_data, eps)

Example calculation:

Show code (15 lines)

den = [10, 2, 0.5, 0.05, 0.001, 0]

# Step 1: Compute median
median = np.median(den)  # = 0.5

# Step 2: Compute MAD
deviations = np.abs(den - median)  # [9.5, 1.5, 0, 0.45, 0.499, 0.5]
mad = np.median(deviations)  # = 0.45

# Step 3: Compute epsilon
eps = 0.1 * mad  # = 0.045

# Step 4: Apply to ratios
ratios = safe_ratio(1, den, eps)

Results:

Denominator	Clipped Den	Ratio (Num=1)	Interpretation
10	10	0.10	Normal
2	2	0.50	Normal
0.5	0.5	2.00	Normal
0.05	0.045	22.22	Guarded
0.001	0.045	22.22	Guarded
0	0.045	22.22	Guarded

Benefits:

✅ Adapts to data scale automatically
✅ Robust to outliers
✅ Principled, not arbitrary
✅ Maintains relative relationships

Using data-driven epsilon based on MAD ensures your ratio stabilization adapts to the actual scale of your data, not arbitrary constants.

Implementation: Complete Robust Ratio Function 🔧

Production-ready version:

Show code (64 lines)

import numpy as np
import pandas as pd

def robust_ratio(numerator, denominator, c=0.1, method='mad', 
                 clip_max=None, log_guards=False):
    """
    Compute robust ratio with data-driven epsilon
    
    Parameters:
    - numerator: array-like numerator values
    - denominator: array-like denominator values
    - c: scaling factor for epsilon (default 0.1)
    - method: method for computing epsilon ('mad' or 'iqr')
    - clip_max: maximum allowed ratio value (optional)
    - log_guards: if True, return count of guarded ratios
    
    Returns:
    - ratios: array of robust ratios
    - guard_count: number of ratios that were guarded (if log_guards=True)
    """
    num = np.asarray(numerator)
    den = np.asarray(denominator)
    
    # Compute epsilon based on method
    if method == 'mad':
        median_den = np.median(den)
        mad = np.median(np.abs(den - median_den))
        eps = c * mad
    elif method == 'iqr':
        q75, q25 = np.percentile(den, [75, 25])
        iqr = q75 - q25
        eps = c * iqr
    else:
        raise ValueError(f"Unknown method: {method}")
    
    # Handle zero epsilon (all denominators same)
    if eps == 0:
        eps = np.finfo(float).eps
    
    # Guard denominators
    den_safe = np.where(np.abs(den) < eps, eps, den)
    
    # Compute ratios
    ratios = num / den_safe
    
    # Clip if requested
    if clip_max is not None:
        ratios = np.clip(ratios, -clip_max, clip_max)
    
    # Count guards
    guard_count = np.sum(np.abs(den) < eps)
    
    if log_guards:
        return ratios, guard_count
    return ratios

# Example usage
numerator = np.array([10, 5, 2, 1, 0.5, 0.1])
denominator = np.array([100, 50, 10, 1, 0.01, 0])

ratios, guards = robust_ratio(numerator, denominator, c=0.1, log_guards=True)
print(f"Ratios: {ratios}")
print(f"Guarded ratios: {guards}/{len(denominator)}")

Output:

Ratios: [0.1, 0.1, 0.2, 1.0, 50.0, 10.0]
Guarded ratios: 2/6

Advanced: Handling Signed Denominators 🔄

Problem: Negative denominators can cause issues

Solution: Use absolute value for epsilon check, preserve sign

Show code (35 lines)

def robust_ratio_signed(num, den, c=0.1):
    """
    Handle signed denominators correctly
    
    For negative denominators:
    - Check |den| < eps
    - If true, replace with sign(den) * eps
    """
    num = np.asarray(num)
    den = np.asarray(den)
    
    # Compute epsilon
    median_den = np.median(np.abs(den))
    mad = np.median(np.abs(np.abs(den) - median_den))
    eps = c * mad
    
    if eps == 0:
        eps = np.finfo(float).eps
    
    # Guard: preserve sign
    den_safe = np.where(
        np.abs(den) < eps,
        np.sign(den) * eps,  # Preserve sign
        den
    )
    
    return num / den_safe

# Example
num = [5, -5, 10]
den = [0.001, -0.001, 0.0001]

ratios = robust_ratio_signed(num, den, c=0.1)
# Result: [positive, negative, positive] - signs preserved!

Real-World Application: Risk Scoring 💼

Scenario: AML (Anti-Money Laundering) risk scoring

Problem:

# Unsafe ratio
risk_score = transaction_amount / avg_account_balance

# Fails when:
# - New account (balance = 0)
# - Low-balance account (balance ≈ 0)
# - Account closure (balance = 0)

Solution:

Show code (25 lines)

def compute_risk_score(amount, avg_balance):
    """
    Compute robust risk score for AML monitoring
    """
    # Use robust ratio
    ratio = robust_ratio(
        amount, 
        avg_balance, 
        c=0.1,  # Conservative epsilon
        clip_max=1000  # Cap at 1000x
    )
    
    # Log guards for monitoring
    _, guard_count = robust_ratio(
        amount, 
        avg_balance, 
        c=0.1, 
        log_guards=True
    )
    
    if guard_count > 0:
        logger.warning(f"Guarded {guard_count} risk scores due to low balances")
    
    return ratio

Benefits:

✅ No crashes on zero balances
✅ Stable scores for low-balance accounts
✅ Monitoring and alerting built-in
✅ Production-ready

Robust ratios act like a radar system, detecting and protecting against dangerous edge cases before they cause system failures.

Common Pitfalls ⚠️

1. Epsilon Too Small 🚫

# Bad: Too small
eps = 1e-9
ratio = num / max(den, eps)

# Problem: Still explodes for very small denominators

Fix: Use data-driven epsilon (MAD-based)

2. Epsilon Too Large 🚫

# Bad: Too large
eps = 1.0
ratio = num / max(den, eps)

# Problem: Distorts real ratios even for normal denominators

Fix: Use small scaling factor (c = 0.1 to 0.5)

3. Ignoring Sign 🚫

# Bad: Doesn't handle negative denominators
den_safe = np.where(den < eps, eps, den)

# Problem: Negative ratios become positive

Fix: Use np.abs(den) < eps and preserve sign

4. No Monitoring 🚫

# Bad: No tracking
ratio = safe_ratio(num, den)

# Problem: Can't detect when guards are triggered frequently

Fix: Add logging and monitoring

5. Fixed Epsilon Across Features 🚫

# Bad: Same epsilon for all features
eps = 1e-6
ratio1 = safe_ratio(num1, den1, eps)
ratio2 = safe_ratio(num2, den2, eps)

# Problem: Different features have different scales

Fix: Compute epsilon per feature

When to Use Robust Ratios 🎯

Perfect For:

✅ Financial ratios

ROE = net_income / equity
ROA = net_income / assets
Debt-to-equity = total_debt / equity

✅ Conversion metrics

CTR = clicks / impressions
Conversion rate = conversions / visits
Bounce rate = bounces / sessions

✅ Growth rates

YoY growth = (current - past) / past
MoM growth = (this_month - last_month) / last_month

✅ Efficiency metrics

Revenue per employee = revenue / employees
Cost per acquisition = marketing_cost / acquisitions

Don't Use When:

❌ Exact zero is meaningful

If denominator = 0 means "not applicable"
→ Use NaN or separate flag, not ratio

❌ Very large denominators dominate

If denominator >> numerator always
→ Consider log ratios or differences instead

❌ Ratios aren't the right metric

If you need absolute differences
→ Use subtraction, not division

Robust ratios balance precision with stability—choosing the right epsilon is like choosing between classical and robust methods.

Pro Tips 💡

1. Choose Scaling Factor Based on Use Case

Show code (9 lines)

# Conservative (financial)
eps = 0.05 * MAD(den)  # c = 0.05

# Moderate (general)
eps = 0.1 * MAD(den)   # c = 0.1

# Aggressive (exploratory)
eps = 0.5 * MAD(den)   # c = 0.5

2. Monitor Guard Frequency

Show code (9 lines)

def robust_ratio_with_monitoring(num, den, c=0.1):
    ratios, guard_count = robust_ratio(num, den, c, log_guards=True)
    guard_pct = 100 * guard_count / len(den)
    
    if guard_pct > 10:  # More than 10% guarded
        logger.warning(f"High guard rate: {guard_pct:.1f}%")
    
    return ratios

3. Use Different Methods for Different Distributions

# Normal-ish distribution
eps = 0.1 * MAD(den)

# Heavy-tailed distribution
eps = 0.1 * IQR(den)  # IQR more robust to outliers

4. Clip Extreme Ratios

# Prevent infinite ratios
ratios = robust_ratio(num, den, c=0.1, clip_max=1000)

5. Test Edge Cases

Show code (12 lines)

# Always test
test_cases = {
    'zeros': ([1, 2, 3], [0, 0, 0]),
    'near_zero': ([1, 2, 3], [1e-10, 1e-9, 1e-8]),
    'mixed': ([1, 2, 3], [10, 0.001, 0]),
    'negative': ([1, -1, 2], [0.001, -0.001, 0.01])
}

for name, (num, den) in test_cases.items():
    ratios = robust_ratio(num, den)
    print(f"{name}: {ratios}")

The Mathematical Beauty 🎓

Why MAD for epsilon?

MAD is a robust measure of scale:

MAD = median(|x_i - median(x)|)

Properties:

Robust to outliers: Unlike standard deviation
Scale-invariant: Adapts to data magnitude
Interpretable: Based on median, not mean
Efficient: O(n log n) computation

The mathematical foundation of robust ratios breaks down complex edge cases into manageable, stable computations.

Connection to other methods:

IQR method: Uses quartiles instead of median
Standard deviation: Less robust but faster
Percentile method: Uses specific percentiles

Why c = 0.1?

Empirical choice based on:

Balance between stability and accuracy
Works well across many domains
Conservative enough to avoid distortion
Aggressive enough to prevent explosions

Summary Table 📋

Aspect	Value
Input	Numerator and denominator arrays
Method	Guard denominators using data-driven epsilon
Epsilon	c × MAD(denominator)
Output	Stable ratios without explosions
Complexity	O(n log n) for MAD computation
Robustness	High (uses median, not mean)
Best for	Ratios with variable denominators
Avoid for	Cases where zero is meaningful

Final Thoughts 🌟

Robust ratios are production insurance 🛡️

Ratios are powerful but need protection
Division-by-zero isn't a math bug—it's a data reality
Robust guardrails make computations stable, continuous, and production-safe

Your ratios should bend, not break. 💪

Tomorrow's Preview: Day 18 — Winsorization & Clipping for Stability! We'll learn how to cap extreme values while preserving distribution shape, perfect for handling outliers in features and targets. 📉🎯

Visualizations 📊

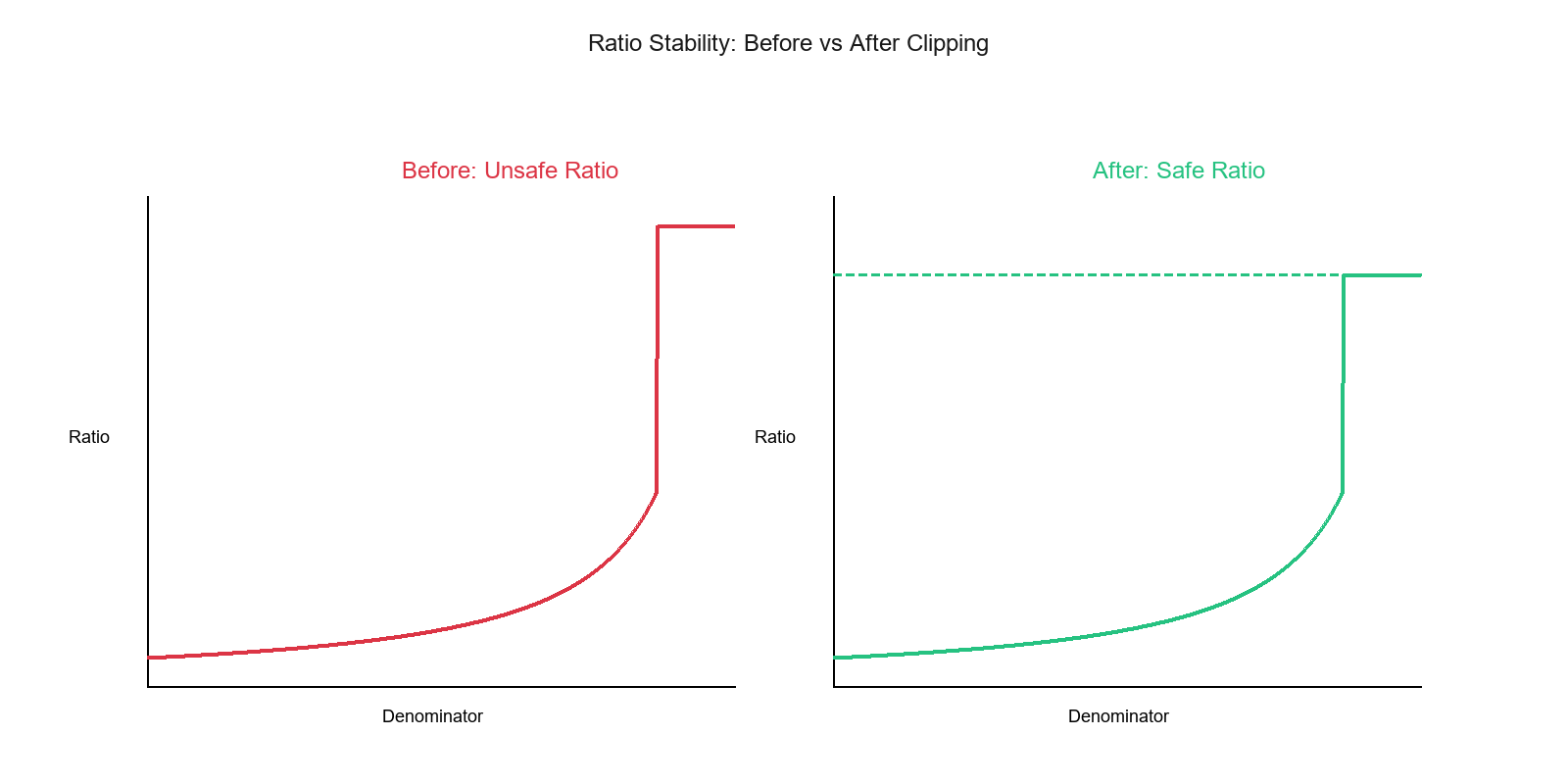
Before: Ratio explodes to infinity near zero. After: Ratio smoothly plateaus at a maximum value, ensuring stable and predictable behavior.

Navigation

Topics

Following

Day 17 — Robust Ratios and Division by Zero

TL;DR