Day 4 — Percentile Rank and Stratification (with Solved Examples)
Ranking and stratifying data for insights!
Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.
Introduction
Percentile ranks provide a powerful way to normalize features onto a common scale, making it easy to combine multiple features and create meaningful stratifications for analysis and sampling.
TL;DR:
Percentile ranks turn any numeric feature into a simple score in [0,1] that says "what fraction of the data is at or below this value."
Because percentile ranks are order-based, they are stable under rescaling and other monotone transforms.
If you combine several features' ranks using min (for AND-like behavior) or max (for OR-like behavior), you get a single score that you can cut into strata (e.g., quartiles/deciles) for sampling, prioritization, or analysis.
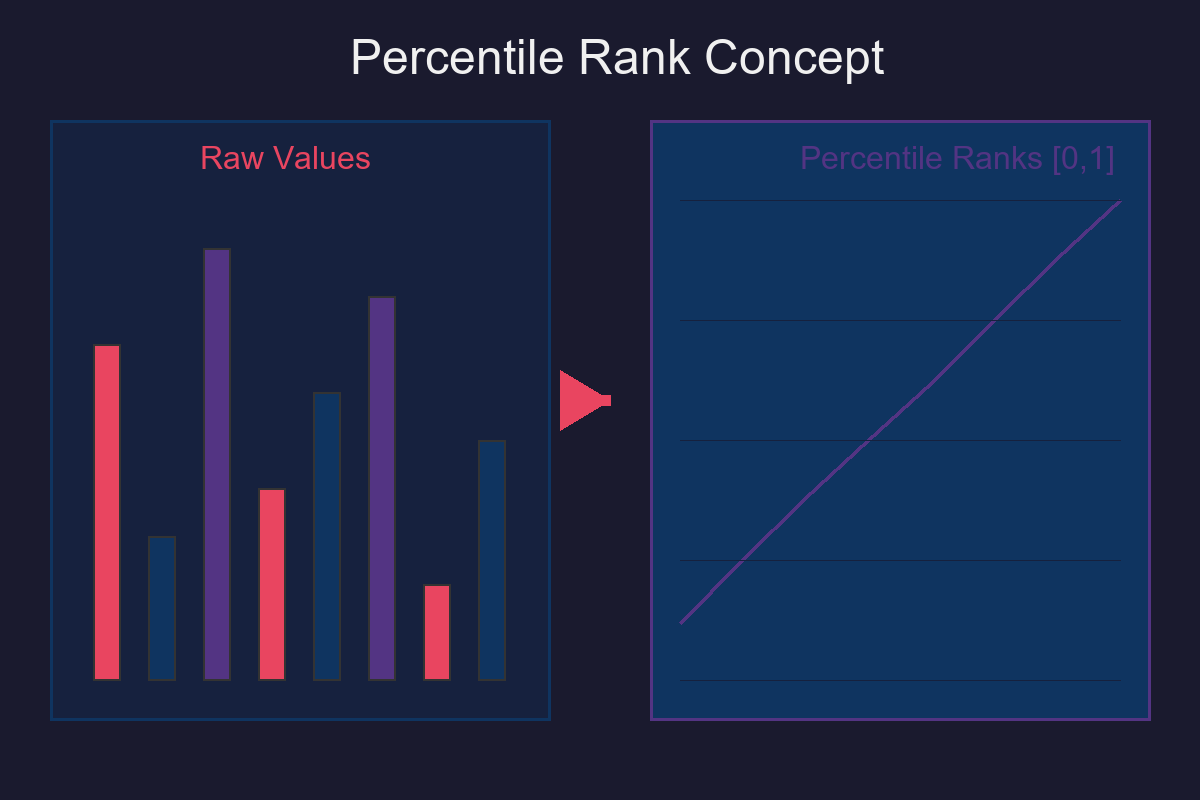
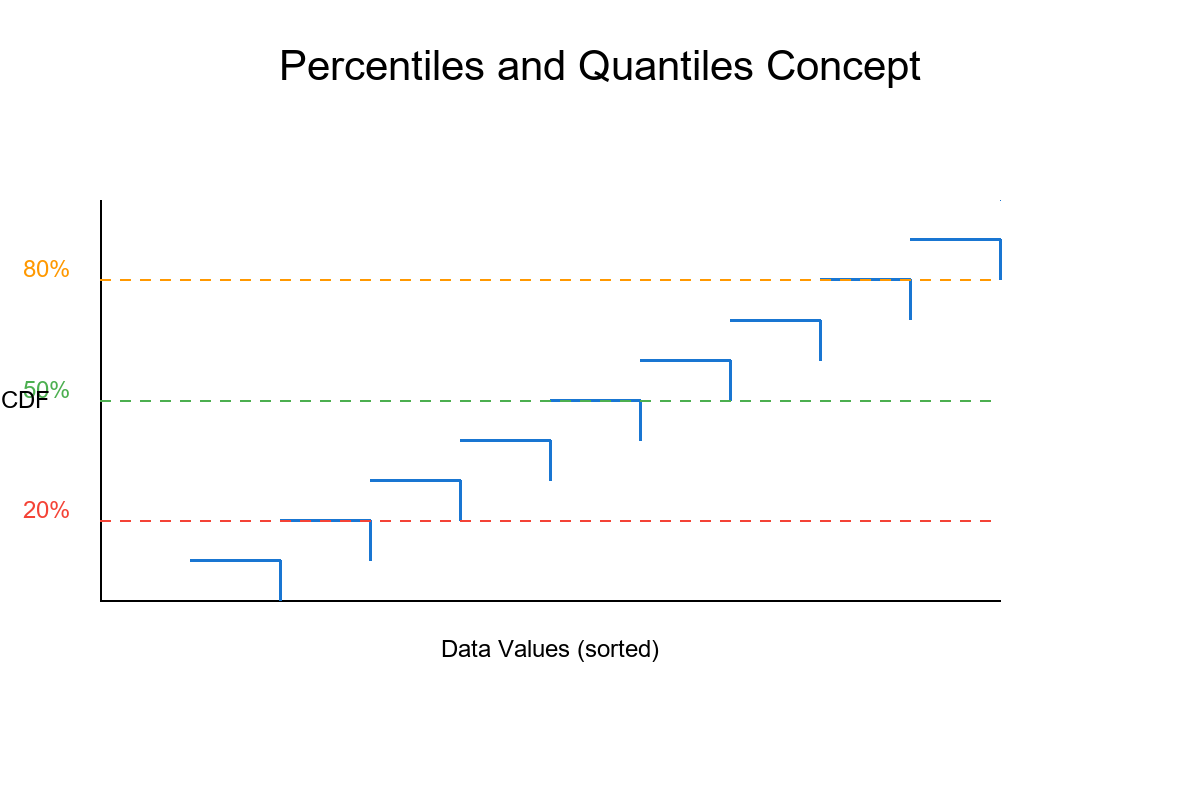
Percentile Rank: A Simple [0,1] Scale
- Given a feature X and a dataset of size n, the percentile rank of a value xᵢ is:
rankᵢ = Fₙ(xᵢ) = (1/n) × (# of values ≤ xᵢ)
- This maps each observation to a number between 0 and 1 (inclusive).
- Properties you get for free:
- Monotonicity (isotonicity): If xᵢ ≤ x, then rankᵢ ≤ rank.
- Invariance to monotone transforms: If f is strictly increasing (e.g., a·x+b with a>0), ranks don't change.
Why this matters: Different features may have different scales or units. Percentile ranks put everything onto the same comparable [0,1] scale, making multi-feature logic easy to reason about.

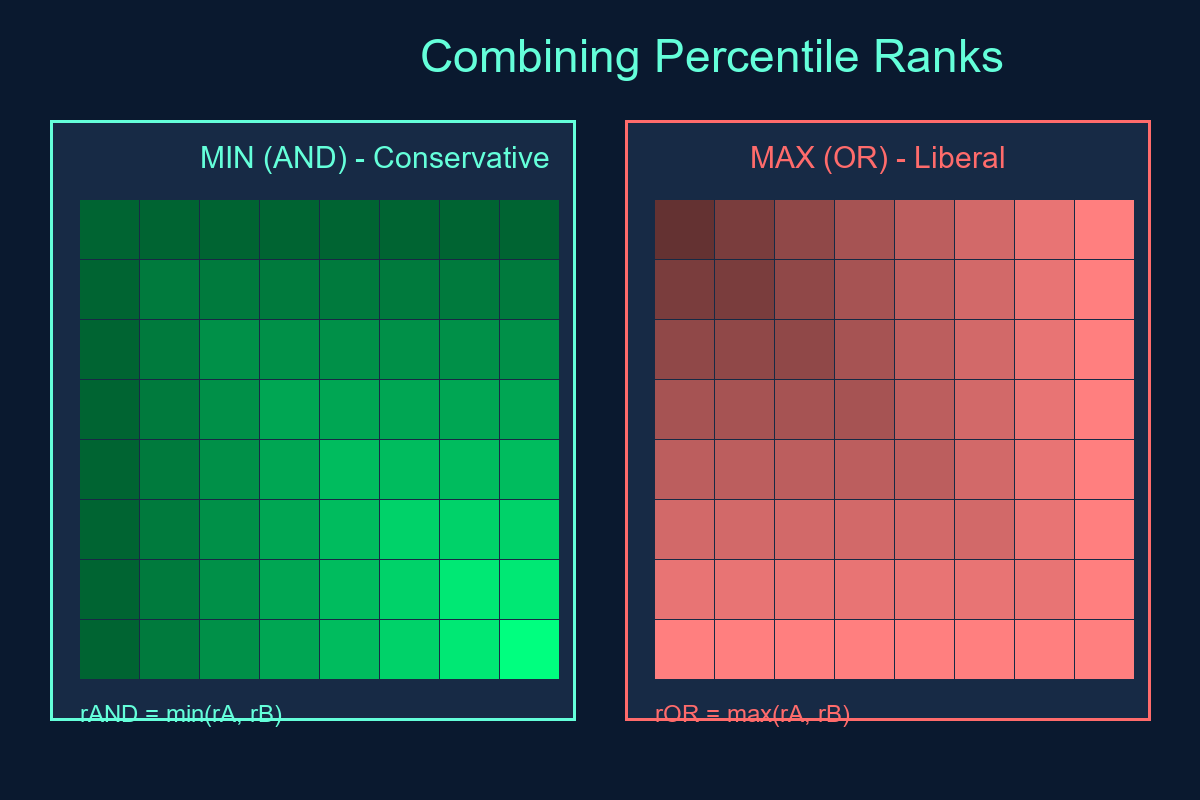
Combining percentile ranks across features
If you have features A and B with ranks rA and rB:
- Conservative (AND-like) combination:
rAND = min(rA, rB)
→ Combined score limited by the weaker (smaller) rank. Safe way to demand "both high."
- Liberal (OR-like) combination:
rOR = max(rA, rB)
→ Combined score benefits from the stronger (larger) rank. Allows "either high."
These match Day 1's logic mapping:
AND ≈ min OR ≈ max
They're simple, monotone, and explainable
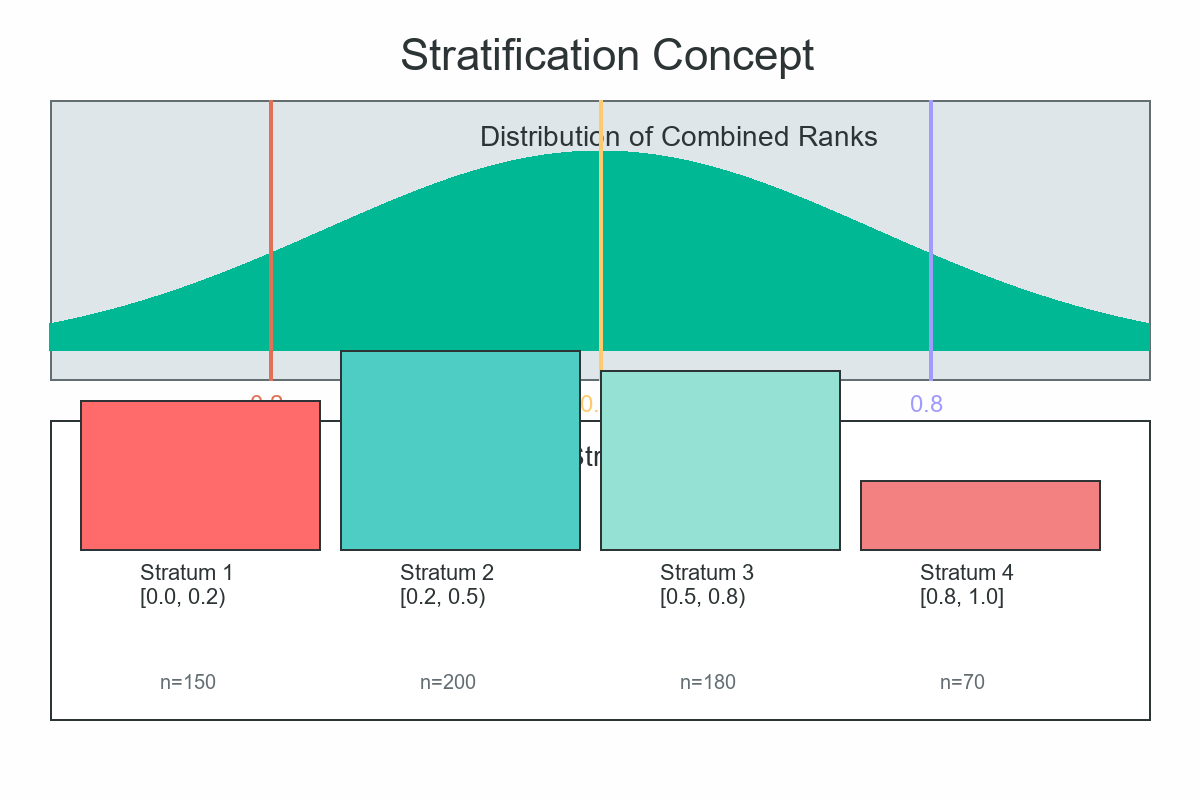
Stratification from Combined Ranks
Once you have a single combined rank per observation (e.g., rAND), split the population into strata:
- Deciles: [0.0, 0.1, 0.2, …, 0.9, 1.0]
- Quartiles: [0.0, 0.25, 0.5, 0.75, 1.0]
- Custom cuts: e.g., [0.0, 0.2, 0.5, 0.8, 1.0]
Use strata to:
- Draw balanced samples
- Prioritize reviews/interventions
- Report performance metrics by difficulty bands
Because ranks are monotone-invariant, your strata stay meaningful even if raw features change scale.
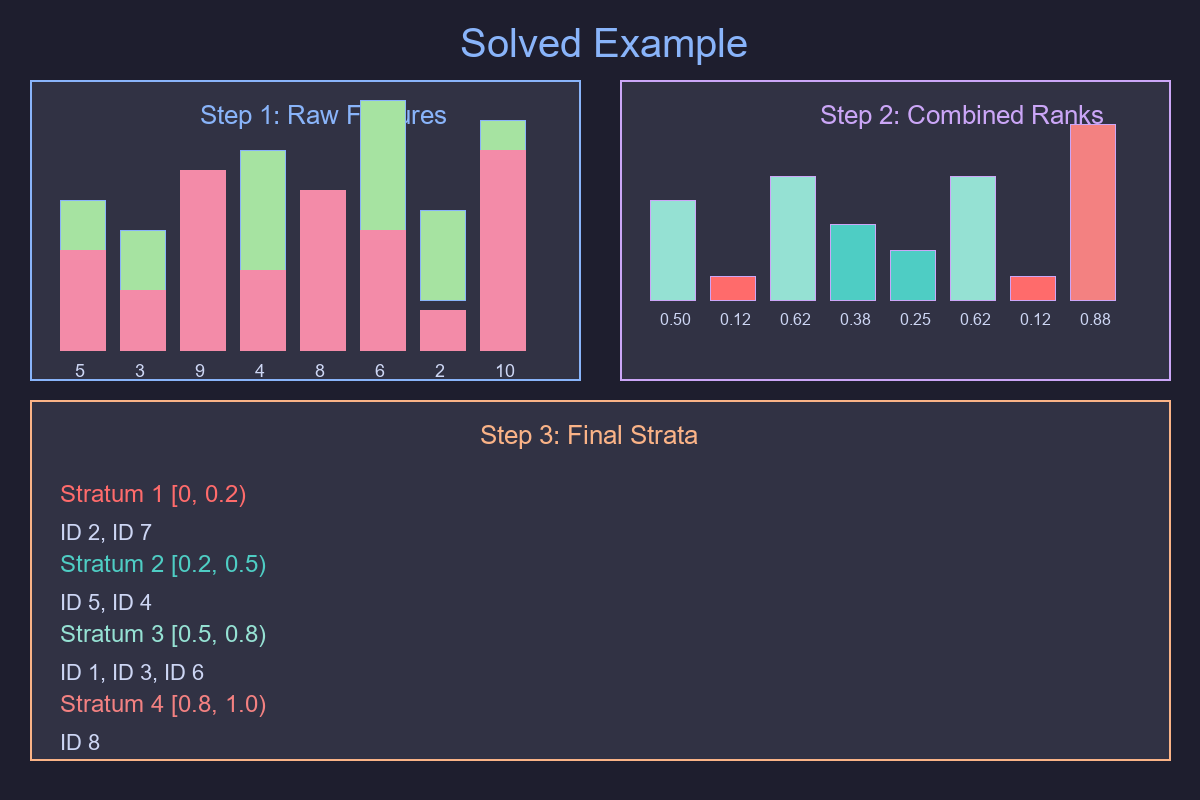
Solved example — From raw features to strata
| id | A | B |
|---|---|---|
| 1 | 10 | 5 |
| 2 | 7 | 3 |
| 3 | 12 | 9 |
| 4 | 15 | 4 |
| 5 | 8 | 8 |
| 6 | 20 | 6 |
| 7 | 9 | 2 |
| 8 | 18 | 10 |
Step 1.: Compute percentile ranks per feature
Use the empirical CDF (rank = i/n). Example (rounded):
| A | rankA | B | rankB |
|---|---|---|---|
| 7 | 0.12 | 2 | 0.12 |
| 8 | 0.25 | 3 | 0.25 |
| 9 | 0.38 | 4 | 0.38 |
| 10 | 0.50 | 5 | 0.50 |
| 12 | 0.62 | 6 | 0.62 |
| 15 | 0.75 | 8 | 0.75 |
| 18 | 0.88 | 9 | 0.88 |
| 20 | 1.00 | 10 | 1.00 |
Step 2.: Combine with min (AND-like) and max (OR-like)
| id | A | B | rA | rB | rAND = min(rA,rB) | rOR = max(rA,rB) |
|---|---|---|---|---|---|---|
| 1 | 10 | 5 | 0.50 | 0.50 | 0.50 | 0.50 |
| 2 | 7 | 3 | 0.12 | 0.25 | 0.12 | 0.25 |
| 3 | 12 | 9 | 0.62 | 0.88 | 0.62 | 0.88 |
| 4 | 15 | 4 | 0.75 | 0.38 | 0.38 | 0.75 |
| 5 | 8 | 8 | 0.25 | 0.75 | 0.25 | 0.75 |
| 6 | 20 | 6 | 1.00 | 0.62 | 0.62 | 1.00 |
| 7 | 9 | 2 | 0.38 | 0.12 | 0.12 | 0.38 |
| 8 | 18 | 10 | 0.88 | 1.00 | 0.88 | 1.00 |
Step 3.: Create strata from rAND
Cuts at 0.2, 0.5, 0.8 →
- Stratum 1: rAND < 0.2 → ids 2, 7
- Stratum 2: 0.2 ≤ rAND < 0.5 → ids 5, 4
- Stratum 3: 0.5 ≤ rAND < 0.8 → ids 1, 3, 6
- Stratum 4: rAND ≥ 0.8 → id 8
Using min is conservative: an observation only scores high if both A and B are high.
Using max is liberal — more points rise into higher strata.
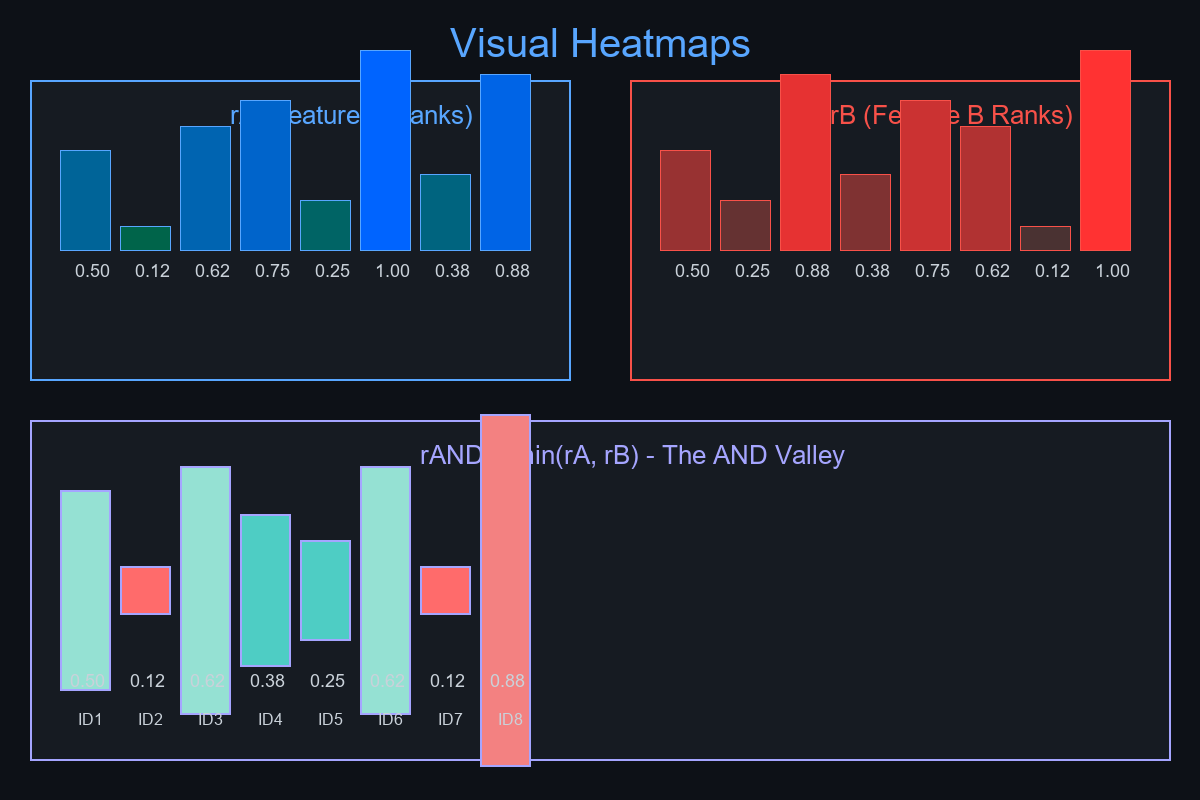
Why "min of ranks" is conservative
- rAND = min(rA, rB) can never exceed either input.
- Raising any rank can only lift (not drop) rAND.
- Thus, demanding high rAND ≈ saying "both inputs are high."

Visual ideas
- Two 2-D heatmaps:
-
rA (x-axis = id, y-axis = rank) and rB similarly.
-
The combined min(rA,rB) mesh — shows the "AND valley."
- Simple bar chart: rAND per id colored by stratum.
Practical tips
- Compute ranks per group for fair comparison (region/time).
- Handle ties consistently (average ranks).
- Pre-decide strata cuts (deciles, quartiles, custom).
- Extend beyond two features:
- rAND = min(r₁,…,rₖ)
- rOR = max(r₁,…,rₖ)
Takeaway
Percentile ranks normalize features onto a common [0,1] scale.
Combining them with min (AND) or max (OR) gives an interpretable, monotone score ideal for sampling, prioritization, and reporting.
Simple Robust Explainable
References
-
Hyndman, R. J., & Fan, Y. (1996). Sample quantiles in statistical packages. The American Statistician, 50(4), 361-365.
-
Serfling, R. J. (2009). Approximation Theorems of Mathematical Statistics. John Wiley & Sons.
-
Mosteller, F., & Tukey, J. W. (1977). Data Analysis and Regression: A Second Course in Statistics. Addison-Wesley.
-
Hoaglin, D. C., Mosteller, F., & Tukey, J. W. (Eds.). (1983). Understanding Robust and Exploratory Data Analysis. John Wiley & Sons.
-
David, H. A., & Nagaraja, H. N. (2003). Order Statistics (3rd ed.). John Wiley & Sons.
-
Parzen, E. (1979). Nonparametric statistical data modeling. Journal of the American Statistical Association, 74(365), 105-121.
-
Koenker, R. (2005). Quantile Regression. Cambridge University Press.
-
Langford, E. (2006). Quartiles in elementary statistics. Journal of Statistics Education, 14(3).
-
Hyndman, R. J. (1996). Computing and graphing highest density regions. The American Statistician, 50(2), 120-126.
-
Cramér, H. (1946). Mathematical Methods of Statistics. Princeton University Press.