Day 8 — Adjusted Boxplot & Medcouple 📊✨

Taming skewed distributions without crying wolf on legitimate extremes.

💡 Note: This article uses technical terms and abbreviations. For definitions, check out the Key Terms & Glossary page.

🎯 Introduction

Regular boxplots assume symmetric data, so a long tail looks suspicious. Real-world datasets—salaries, housing prices, reaction times—are often skewed. The adjusted boxplot fixes this by combining Tukey-style fences with the medcouple, a robust skewness statistic.

TL;DR:

• Medcouple measures skewness on a scale from −1 → +1.
• Adjusted fences use exponential factors so the long tail gets extra space.
• Positively skewed data widens the upper fence and tightens the lower fence (and vice versa).
• Use adjusted boxplots when histograms look lopsided or domain knowledge says “long tail is normal”.

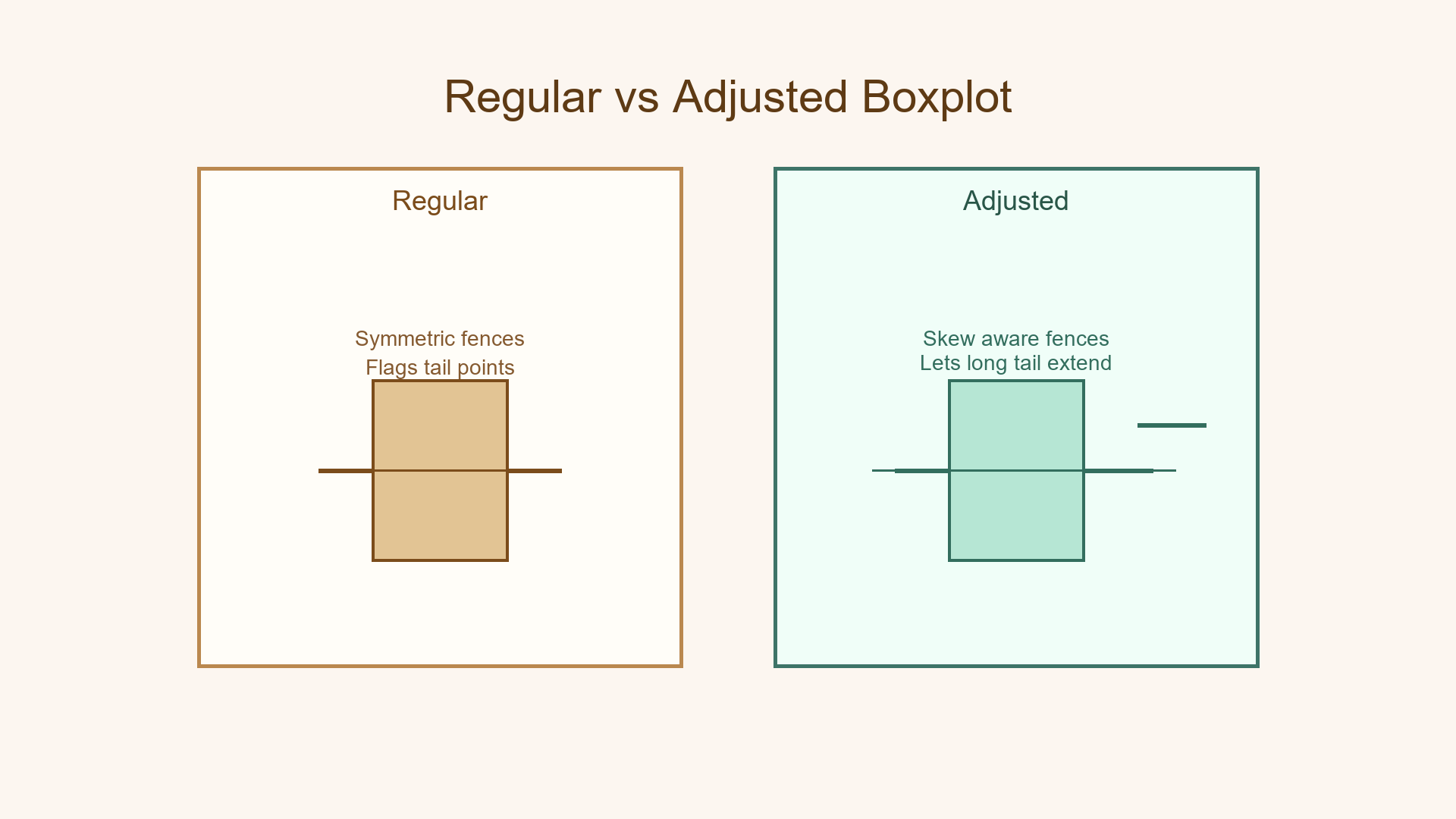
🤔 The Problem with Regular Boxplots

Imagine company salaries: most lie between ₹40k–₹80k, yet one executive earns ₹1600k. A traditional boxplot calls that an outlier because it places equal weight on both tails. The result: normal tail behavior is mislabelled as noise.

Why symmetric fences fail

• Traditional fences: Lower = Q₁ − 1.5 × [IQR](/key) and Upper = Q₃ + 1.5 × IQR
• Works brilliantly when the distribution is balanced.
• Breaks when a tail is naturally long—think incomes, clicks, insurance claims.

Regular boxplots think “extreme on either side” is equally likely; skewed data disagrees.

🎯 Enter the Adjusted Boxplot

The adjusted boxplot tweaks Tukey’s fences with an exponential factor driven by the medcouple. More skew means more asymmetry in the allowable range.

Smart guard analogy

• Regular guard: “Tall or short? Either way you look suspicious.”
• Adjusted guard: “Most folks are tall today; short people stand out more than tall ones.”

📐 Meet the Medcouple (MC)

The medcouple is a robust skewness statistic that compares symmetric pairs around the median. It ignores extreme values and captures how one tail spreads relative to the other.

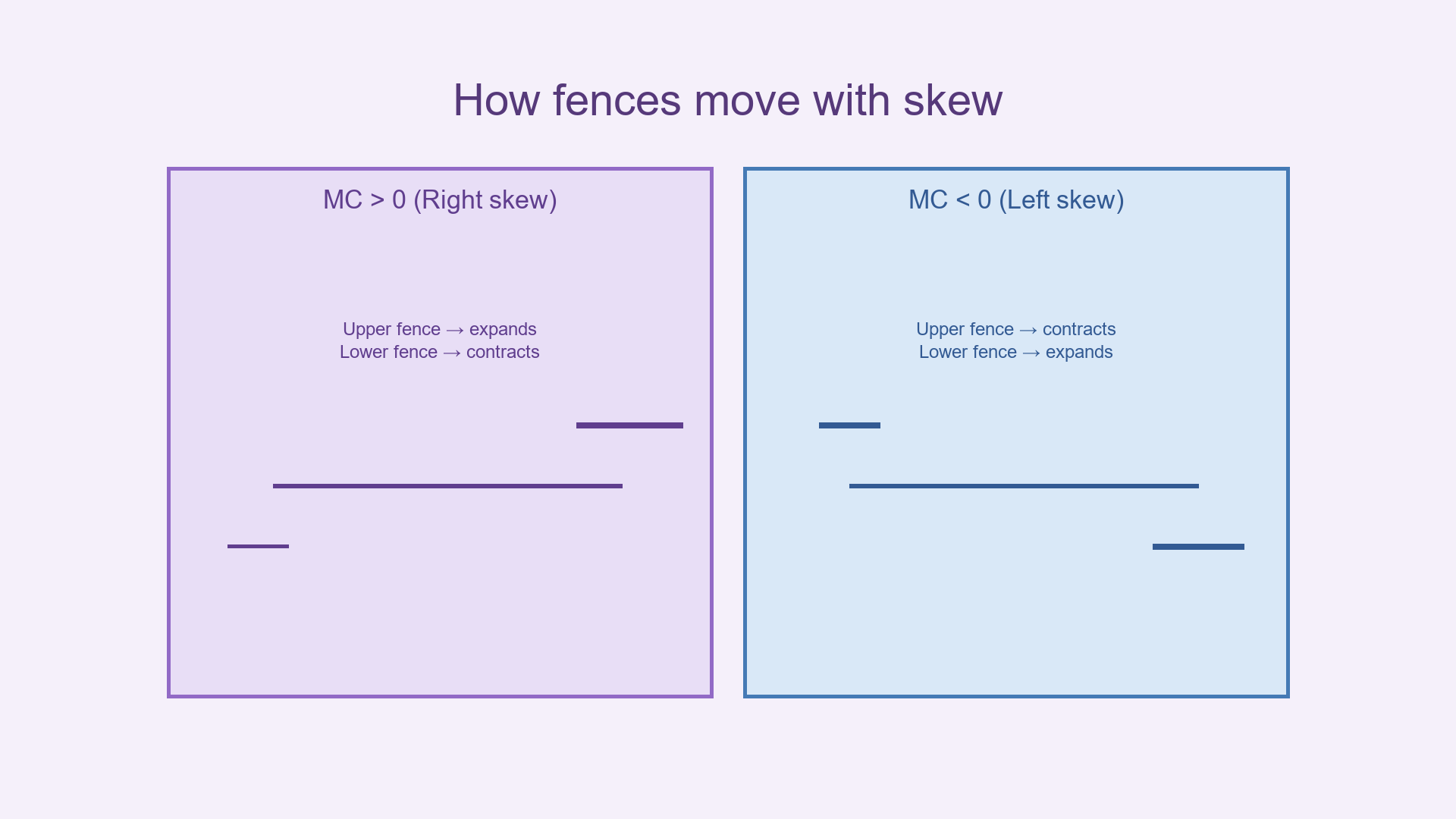
• MC ≈ 0 → roughly symmetric.
• MC > 0 → positively skewed (long right tail).
• MC < 0 → negatively skewed (long left tail).

MC = median of h(xᵢ, xⱼ)

where h(xᵢ, xⱼ) = ((xⱼ - median) - (median - xᵢ)) / (xⱼ - xᵢ)

Robust means the statistic resists the influence of single extreme values—perfect for skewed data.

🚧 How the Adjusted Fences Work

Traditional fences use a fixed multiplier. Adjusted fences multiply 1.5 × IQR by an exponential function of the medcouple:

Lower fence = Q₁ − 1.5 × exp(−3.5 × MC) × [IQR](/key)
Upper fence = Q₃ + 1.5 × exp(+4.0 × MC) × [IQR](/key)

• Positive MC (right skew): exp(+4.0 × MC) explodes, stretching the upper fence; exp(−3.5 × MC) shrinks, tightening the lower fence.
• Negative MC (left skew): the behavior flips—lower fence loosens, upper fence tightens.

🏡 Worked Example — House Prices

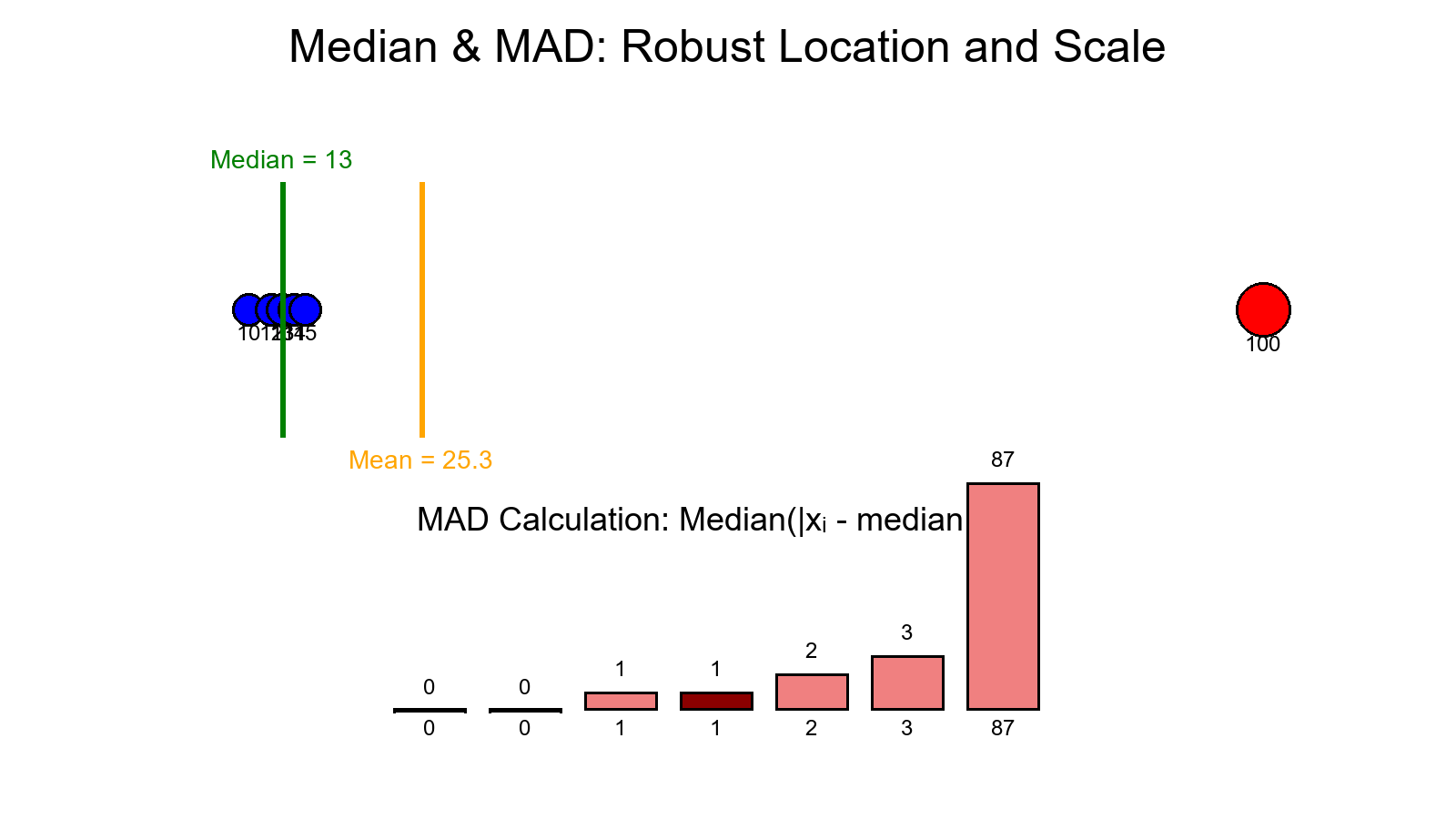
Dataset (₹ in thousands): [150, 180, 200, 220, 250, 280, 320, 400, 650, 1200]

[Q₁](/key) = 200,  [Q₂](/key) = 265,  [Q₃](/key) = 400
[IQR](/key) = 200
Medcouple ≈ 0.35 (right skew)

Traditional fences

Lower = 200 − 1.5 × 200 = −100
Upper = 400 + 1.5 × 200 = 700 → flags 1200 as an outlier ❌

Adjusted fences

Lower = 200 − 1.5 × exp(−3.5 × 0.35) × 200 ≈ 112
Upper = 400 + 1.5 × exp(4.0 × 0.35) × 200 ≈ 1618

No outliers detected ✅ — the long right tail is normal for property values.

🔧 Pseudocode Implementation

def adjusted_boxplot_outliers(data):
    Q1, Q3 = compute_quartiles(data)
    IQR = Q3 - Q1
    MC = compute_medcouple(data)

    lower = Q1 - 1.5 * math.exp(-3.5 * MC) * IQR
    upper = Q3 + 1.5 * math.exp(4.0 * MC) * IQR

    return [x for x in data if x < lower or x > upper]

Tools like adjusted_boxplot_outliers in our toolkit automate the math while you focus on interpretation.

🎯 When to Switch Boxplots

Use adjusted boxplots when:

• Histograms or density plots reveal skewness.
• Domain knowledge screams “long tail is normal” (salaries, prices, insurance claims).
• Traditional boxplots call too many valid values outliers.

Stick with regular boxplots when:

• Data is roughly symmetric or sample size is tiny (<20).
• You need a quick-and-dirty check for any extreme value.

🌟 Takeaway

• The medcouple captures skewness without being tricked by outliers.
• Adjusted boxplots expand and contract fences intelligently.
• Long tails stop masquerading as anomalies; true anomalies still pop.

🔭 Coming Up Next

Day 9 — Local Outlier Factor (LOF) explores density-based detection so you can catch anomalies hiding in neighborhoods.

📚 References

• Annick Brys, Mia Hubert, and Peter Rousseeuw (2004). “A Robust Measure of Skewness.” Journal of Computational and Graphical Statistics.
• Rousseeuw, P. J., & Hubert, M. (2011). “Robust Statistics for Outlier Detection.” Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery.
• Hubert, M., Vandervieren, E. (2008). “An Adjusted Boxplot for Skewed Distributions.” Computational Statistics & Data Analysis.

🎉 You Made It — Day 8

Thanks for sticking with the journey! Every day adds another robust tool to your kit.

✨ In one line: Adjusted boxplots plus the medcouple let you respect skewed data while still catching the truly weird points.